题目内容
已知函数f(x)=|3-
|,x∈(0,+∞).
(1)写出f(x)的单调区间;
(2)是否存在实数a,b(0<a<b)使函数y=f(x)定义域值域均为[a,b],若存在,求出a,b的值,若不存在,请说明理由.
| 1 | x |
(1)写出f(x)的单调区间;
(2)是否存在实数a,b(0<a<b)使函数y=f(x)定义域值域均为[a,b],若存在,求出a,b的值,若不存在,请说明理由.
分析:(1)先将原含有绝对值的函数化成分段函数的形式,再画出其图象,观察图象可得f(x)的单调区间;
(2)可假设存在实数a,b,使得y=f(x)的定义域和值域都是[a,b],由此出发探究a,b的可能取值,可分三类:当a≥
时,当0<a<
<b时,当b≤
时,分别建立方程,寻求a,b的可能取值,若能求出这样的实数,则说明存在,否则说明不存在.
(2)可假设存在实数a,b,使得y=f(x)的定义域和值域都是[a,b],由此出发探究a,b的可能取值,可分三类:当a≥
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答: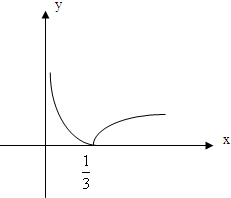 解:(1)易知 f(x)=
解:(1)易知 f(x)=
即单调减区间为(0,
);单调增区间为(
,+∞)
(2)因为f(x)=|3-
|的定义域与值域均为[a,b]
①当a≥
时,f(x)在区间[a,b]上递增
所以
⇒
⇒
;
②当0<a<
<b时,f(x)在[a,
)递减,在[
,b]上递增
值域为[a,b],即a=0,与题矛盾;
③当b≤
时,f(x)在[a,b]上递减
所以
⇒
⇒不合题意
综上所述,a=
,b=
.
 解:(1)易知 f(x)=
解:(1)易知 f(x)=
|
即单调减区间为(0,
| 1 |
| 3 |
| 1 |
| 3 |
(2)因为f(x)=|3-
| 1 |
| x |
①当a≥
| 1 |
| 3 |
所以
|
|
|
②当0<a<
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
值域为[a,b],即a=0,与题矛盾;
③当b≤
| 1 |
| 3 |
所以
|
|
综上所述,a=
3-
| ||
| 2 |
3+
| ||
| 2 |
点评:本题的考点是函数与方程的综合应用,考察了绝对值函数,函数的定义域、值域,解题的关键是理解题意,将问题正确转化,进行分类讨论探究,本题考察了分类讨论的思想,方程的思想,考察了推理判断能力,是一道综合性较强的题,思维难度大,解题时要严谨,本题易因为考虑不完善出错.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|