题目内容
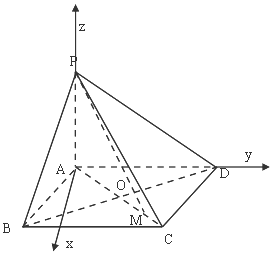
【题目】如图,已知四棱锥P﹣ABCD中,PA⊥BD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b,AC与BD交于点O,M为OC的中点. 
(1)求证:平面PAC⊥平面ABCD;
(2)若∠PAC=90°,二面角O﹣PM﹣D的正切值为 ![]() ,求a:b的值.
,求a:b的值.
【答案】
(1)证明:因为底面ABCD是菱形,所以AC⊥BD,
又PA⊥BD,PA∩AC=A,
所以BD⊥面PAC,
又因为 PD面ABCD,
所以 平面PAC⊥平面ABCD
(2)解:由∠PAC=90°可知PA⊥AC,
又由(1)可知平面PAC⊥平面ABCD
平面PAC∩平面ABCD=AC,
所以 PA⊥平面ABCD,
故如图,
以A为坐标原点,AD,AP所在直线分别为y,z轴建立空间直角坐标系,
则P(0,0,b),D(0,a,0),M( ![]() ,
, ![]() ,0),O(
,0),O( ![]() ,
, ![]() ,0)
,0)
从而 ![]() =(0,a,﹣b),
=(0,a,﹣b), ![]() =(
=( ![]() a,
a, ![]() ,﹣b),
,﹣b),
![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0),
因为BD⊥面PAC,所以平面PMO的一个法向量为 ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0),
设平面PMD的法向量为 ![]() =(x,y,z),
=(x,y,z),
由 ![]() ,
, ![]() ,得
,得
 ,
,
令y=b,得x= ![]() ,z=a,即
,z=a,即 ![]() ,
,
设 ![]() 与
与 ![]() 的夹角为θ,则二面角O﹣PM﹣D的大小与θ相等,
的夹角为θ,则二面角O﹣PM﹣D的大小与θ相等,
由 ![]() ,得
,得 ![]()

化简得 4b=3a,即a:b=4:3
【解析】(1)推导出AC⊥BD,PA⊥BD,由此能证明平面PAC⊥平面ABCD.(2)以A为坐标原点,AD,AP所在直线分别为y,z轴建立空间直角坐标系,利用利用向量法能求出a:b的值.

【题目】教育部记录了某省2008到2017年十年间每年自主招生录取的人数![]() 为方便计算,2008年编号为1,2009年编号为2,
为方便计算,2008年编号为1,2009年编号为2,![]() ,2017年编号为10,以此类推
,2017年编号为10,以此类推![]() 数据如下:
数据如下:
年份编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人数 | 3 | 5 | 8 | 11 | 13 | 14 | 17 | 22 | 30 | 31 |
![]() Ⅰ
Ⅰ![]() 根据前5年的数据,利用最小二乘法求出y关于x的回归方程
根据前5年的数据,利用最小二乘法求出y关于x的回归方程![]() ,并计算第8年的估计值和实际值之间的差的绝对值;
,并计算第8年的估计值和实际值之间的差的绝对值;
![]() Ⅱ
Ⅱ![]() 根据
根据![]() Ⅰ
Ⅰ![]() 所得到的回归方程预测2018年该省自主招生录取的人数.
所得到的回归方程预测2018年该省自主招生录取的人数.
其中![]() ,
,![]()