题目内容
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知向量 ![]() =(2a,1),
=(2a,1), ![]() =(2b﹣c,cosC),且
=(2b﹣c,cosC),且 ![]() ∥
∥ ![]() .
.
(Ⅰ)求角A的大小;
(Ⅱ)若 ![]() ,求b+c的取值范围.
,求b+c的取值范围.
【答案】解:(Ⅰ)向量 ![]() =(2a,1),
=(2a,1), ![]() =(2b﹣c,cosC),且
=(2b﹣c,cosC),且 ![]() ∥
∥ ![]() ;∴2acosC﹣(2b﹣c)=0,
;∴2acosC﹣(2b﹣c)=0,
即2acosC=2b﹣c;
由正弦定理得,2sinAcosC=2sinB﹣sinC,
即2sinAcosC=2sin(A+C)﹣sinC,
∴2sinAcosC=2sinAcosC+2cosAsinC﹣sinC,
化简得2cosAsinC=sinC,
即cosA= ![]() ;
;
又A∈(0,π),
∴A= ![]() ;
;
(Ⅱ)△ABC中,A= ![]() ,a=
,a= ![]() ,
,
设△ABC外接圆的直径为2r,
由正弦定理得2r= ![]() =
= ![]() =2,
=2,
∴b+c=2sinB+2sinC
=2[sin(120°﹣C)+sinC]
=4sin60°cos(60°﹣C)
=2 ![]() cos(60°﹣C);
cos(60°﹣C);
∵﹣60°<60°﹣C<60°,
∴1≥cos(60°﹣C)> ![]() ,
,
∴2 ![]() ≥2
≥2 ![]() cos(60°﹣C)>
cos(60°﹣C)> ![]() ,
,
即b+c的取值范围是( ![]() ,2
,2 ![]() ]
]
【解析】(Ⅰ)根据平面向量的坐标运算与共线定理,利用正弦定理与三角形的内角和定理,即可求出A的值;(Ⅱ)利用正弦定理求出b+c的表达式,再根据角C的取值范围,即可求出b+c的取值范围.
【考点精析】通过灵活运用正弦定理的定义和余弦定理的定义,掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 即可以解答此题.
即可以解答此题.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案【题目】近年空气质量逐步恶化,雾霾天气现象增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对入院的50人进行问卷调查,得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
(Ⅰ)用分层抽样的方法在患心肺疾病的人群中抽6人,其中男性抽多少人?
(Ⅱ)在上述抽取的6人中选2人,求恰好有1名女性的概率;
(Ⅲ)为了研究心肺疾病是否与性别有关,请计算出统计量![]() ,你有多大把握认为心肺疾病与性别有关?(结果保留三个有效数字)
,你有多大把握认为心肺疾病与性别有关?(结果保留三个有效数字)
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024/p> | 6.635 | 7.879 | 10.828 |
参考公式: ![]() ,其中
,其中![]() .
.
【题目】小明在石家庄市某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前55单没有奖励,超过55单的部分每单奖励12元.
(Ⅰ)请分别求出甲、乙两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
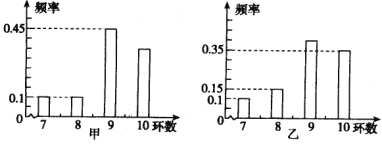
(Ⅱ)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的直方图,其中当某天的派送量指标在(![]() ,
,![]() ](n=1,2,3,4,5)时,日平均派送量为50+2n单.若将频率视为概率,回答下列问题:
](n=1,2,3,4,5)时,日平均派送量为50+2n单.若将频率视为概率,回答下列问题:

①根据以上数据,设每名派送员的日薪为X(单位:元),试分别求出甲、乙两种方案的日薪X的分布列,数学期望及方差;
②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由。
(参考数据:0.62=0.36,1.42=1.9 6,2.6 2=6.76,3.42=1 1.56,3.62=12.96,4.62=21.16,15.62=243.36,20.42=416.16,44.42=1971.36)
【答案】(Ⅰ)甲方案的函数关系式为: ![]() ,乙方案的函数关系式为:
,乙方案的函数关系式为:![]() ;(Ⅱ)①见解析,②见解析.
;(Ⅱ)①见解析,②见解析.
【解析】
(Ⅰ)由题意可得甲方案中派送员日薪![]() (单位:元)与送单数
(单位:元)与送单数![]() 的函数关系式为:
的函数关系式为: ![]() , 乙方案中派送员日薪
, 乙方案中派送员日薪![]() (单位:元)与送单数
(单位:元)与送单数![]() 的函数关系式为:
的函数关系式为:![]() .
.
(Ⅱ)①由题意求得X的分布列,据此计算可得![]() ,
,![]() ,
,![]() .
.
②答案一:由以上的计算可知,![]() 远小于
远小于![]() ,即甲方案日工资收入波动相对较小,所以小明应选择甲方案.
,即甲方案日工资收入波动相对较小,所以小明应选择甲方案.
答案二:由以上的计算结果可以看出,![]() ,所以小明应选择乙方案.
,所以小明应选择乙方案.
(Ⅰ)甲方案中派送员日薪![]() (单位:元)与送单数
(单位:元)与送单数![]() 的函数关系式为:
的函数关系式为: ![]() ,
,
乙方案中派送员日薪![]() (单位:元)与送单数
(单位:元)与送单数![]() 的函数关系式为:
的函数关系式为:![]()
(Ⅱ)①由已知,在这100天中,该公司派送员日平均派送单数满足如下表格:
单数 | 52 | 54 | 56 | 58 | 60 |
频率 | 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
所以![]() 的分布列为:
的分布列为:
| 152 | 154 | 156 | 158 | 160 |
| 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
所以![]()
所以![]() 的分布列为:
的分布列为:
| 140 | 152 | 176 | 200 |
| 0.5 | 0.2 | 0.2 | 0.1 |
所以![]()
![]()
②答案一:由以上的计算可知,虽然![]() ,但两者相差不大,且
,但两者相差不大,且![]() 远小于
远小于![]() ,即甲方案日工资收入波动相对较小,所以小明应选择甲方案.
,即甲方案日工资收入波动相对较小,所以小明应选择甲方案.
答案二:由以上的计算结果可以看出,![]() ,即甲方案日工资期望小于乙方案日工资期望,所以小明应选择乙方案.
,即甲方案日工资期望小于乙方案日工资期望,所以小明应选择乙方案.
【点睛】
本题主要考查频率分布直方图,数学期望与方差的含义与实际应用等知识,意在考查学生的转化能力和计算求解能力.
【题型】解答题
【结束】
20
【题目】已知椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,且离心率为
(a>b>0)的左、右焦点分别为F1,F2,且离心率为![]() ,M为椭圆上任意一点,当∠F1MF2=90°时,△F1MF2的面积为1.
,M为椭圆上任意一点,当∠F1MF2=90°时,△F1MF2的面积为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点A是椭圆C上异于椭圆顶点的一点,延长直线AF1,AF2分别与椭圆交于点B,D,设直线BD的斜率为k1,直线OA的斜率为k2,求证:k1·k2等于定值.