题目内容
15．若a，b，c均为实数，且ab＜0，则下列不等式正确的是（ ）| A． | |a+b|＞|a-b| | B． | |a|+|b|＞|a-b| | C． | |a-c|≤|a-b|+|b-c| | D． | |a-b|＜|a|-|b| |
分析 不妨令a=2，b=-1，代入各个选项检验可得A、B、D不成立，从而得出结论．
解答 解：不妨令a=2，b=-1，代入各个选项检验可得A、B、D不成立，
由绝对值三角不等式，可得|a-c|=|（a-b）+（b-c|≤|a-b|+|b-c|，故C成立，
故选：C．
点评 本题主要考查绝对值不等式的应用，绝对值三角不等式；通过举反例来说明某个结论不成立，是一种简单有效的方法，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
5．已知实数x，y满足$\left\{\begin{array}{l}y≥1\\ y≤2x-1\\ x+y≤m\end{array}\right.$，如果目标函数z=x-y的最小值为-2，则实数m的值为（ ）
| A． | 0 | B． | 2 | C． | 4 | D． | 8 |
6．已知I为△ABC所在平面上的一点，且AB=c，AC=b，BC=a．若a$\overrightarrow{IA}$+b$\overrightarrow{IB}$+c$\overrightarrow{IC}$=$\overrightarrow{0}$，则I一定是△ABC的（ ）
| A． | 垂心 | B． | 内心 | C． | 外心 | D． | 重心 |
20．设a，b∈R，则a2（a-b）＞0是a＞b的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不必要也不充分条件 |
4．已知△ABC中，内角A，B，C所对的边长分别为a，b，c．若a=2bcosA，B=$\frac{π}{3}$，c=1，则△ABC的面积等于（ ）
| A． | $\frac{{\sqrt{3}}}{8}$ | B． | $\frac{{\sqrt{3}}}{6}$ | C． | $\frac{{\sqrt{3}}}{4}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
5．
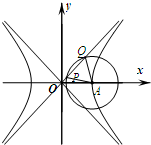如图，已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的某渐近线交于两点P，Q．若∠PAQ=60°且$\overrightarrow{OQ}$=4$\overrightarrow{OP}$，则双曲线C的离心率为（ ）
如图，已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的某渐近线交于两点P，Q．若∠PAQ=60°且$\overrightarrow{OQ}$=4$\overrightarrow{OP}$，则双曲线C的离心率为（ ）| A． | $\sqrt{3}$ | B． | $\frac{2\sqrt{13}}{5}$ | C． | $\frac{\sqrt{7}}{2}$ | D． | $\frac{2\sqrt{3}}{3}$ |