题目内容
3.在O点测量到远处有一物体在做匀速直线运动,开始时该物体位于P点,一分钟后,其位置在Q点,且∠POQ=90°,再过两分钟后,该物体位于R点,且∠QOR=30°,则tan∠OPQ的值为$\frac{2\sqrt{3}}{3}$.分析 利用正弦定理分别在△RQO和△RPO中分别表示出OQ和OP,进而根据tan∠OPQ=$\frac{OQ}{OP}$求得答案.
解答 
解:依题意可知RQ=2QP,
在△RQO中,$\frac{OQ}{sinR}$=$\frac{RQ}{sin30°}$,
OQ=$\frac{RQ}{sin30°}$•sinR,
同理在△RPO中,OP=$\frac{RP}{sin120°}$•sinR,
tan∠OPQ=$\frac{OQ}{OP}$=$\frac{\frac{RQ}{sin30°}}{\frac{RP}{sin120°}}$=$\frac{RQ}{sin30°}$•$\frac{sin120°}{RP}$=$\frac{2}{3}$×$\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}$=$\frac{2\sqrt{3}}{3}$.
点评 本题主要考查了正弦定理的运用.解决问题的关键是运用sinR作为中间量来解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知{an}为等差数列,Sn为其前n项和.若a1=12,S6=S11,则必有( )
| A. | a17=0 | B. | a6+a12=0 | C. | S17>0 | D. | a9<0 |
18.已知集合A={x2-x-2>0},集合B={x||x-a|<3},若A∪B=R,则实数a的取值范围是( )
| A. | [1,2] | B. | (-1,2) | C. | [-1,2] | D. | (-2,1) |
15.若a,b,c均为实数,且ab<0,则下列不等式正确的是( )
| A. | |a+b|>|a-b| | B. | |a|+|b|>|a-b| | C. | |a-c|≤|a-b|+|b-c| | D. | |a-b|<|a|-|b| |
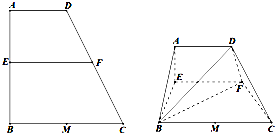 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.