题目内容
10.已知F1,F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,B是椭圆的上顶点,BF2的延长线交椭圆于点A,过点A垂直于x轴的直线交椭圆于点C.(1)若点C坐标为$(\frac{4}{3},\frac{1}{3})$,且|BF2|=$\sqrt{2}$,求椭圆的方程;
(2)若F1C⊥AB,求椭圆的离心率.
分析 (1)根据椭圆的方程和性质,建立方程关系即可求出a,b的值.
(2)求出C的坐标,利用F1C⊥AB建立斜率之间的关系,解方程即可求出e的值.
解答 解:(1)∵C的坐标为($\frac{4}{3}$,$\frac{1}{3}$),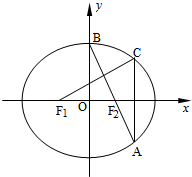
∴$\frac{\frac{16}{9}}{{a}^{2}}$+$\frac{\frac{1}{9}}{{b}^{2}}$=1,即$\frac{16}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=9,
∵|BF2|=$\sqrt{2}$,a2=b2+c2,
∴a2=($\sqrt{2}$)2=2,即b2=1,
则椭圆的方程为$\frac{{x}^{2}}{2}$+y2=1.
(2)设F1(-c,0),F2(c,0),
∵B(0,b),
∴直线BF2:y=-$\frac{b}{c}$x+b,代入椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)得
($\frac{1}{{a}^{2}}$+$\frac{1}{{c}^{2}}$)x2-$\frac{2}{c}$x=0,
解得x=0,或x=$\frac{2{a}^{2}c}{{a}^{2}+{c}^{2}}$,
∵A($\frac{2{a}^{2}c}{{a}^{2}+{c}^{2}}$,$\frac{b({c}^{2}-{a}^{2})}{{a}^{2}+{c}^{2}}$),且A,C关于x轴对称,
∴C($\frac{2{a}^{2}c}{{a}^{2}+{c}^{2}}$,-$\frac{b({c}^{2}-{a}^{2})}{{a}^{2}+{c}^{2}}$),
则${k}_{{F}_{1}C}$=-$\frac{\frac{b({c}^{2}-{a}^{2})}{{a}^{2}+{c}^{2}}}{\frac{2{a}^{2}c}{{a}^{2}+{c}^{2}}+c}$=$\frac{{a}^{2}b-b{c}^{2}}{3{a}^{2}c+{c}^{3}}$,
∵F1C⊥AB,
∴$\frac{{a}^{2}b-b{c}^{2}}{3{a}^{2}c+{c}^{3}}$•(-$\frac{b}{c}$)=-1,
由b2=a2-c2得$\frac{{c}^{2}}{{a}^{2}}$=$\frac{1}{5}$,
即e=$\frac{\sqrt{5}}{5}$.
点评 本题主要考查圆锥曲线的综合问题,要求熟练掌握椭圆方程的求法以及直线垂直和斜率之间的关系,运算量较大.

 阅读快车系列答案
阅读快车系列答案| A. | [1,2] | B. | (-1,2) | C. | [-1,2] | D. | (-2,1) |
| A. | |a+b|>|a-b| | B. | |a|+|b|>|a-b| | C. | |a-c|≤|a-b|+|b-c| | D. | |a-b|<|a|-|b| |
 如图,已知切线PA切圆于点A,割线PBC分别交圆于点B,C,点D在线段BC上,且DC=2BD,∠BAD=∠PAB,$PA=2\sqrt{10}$,PB=4,则线段AB的长为2$\sqrt{3}$.
如图,已知切线PA切圆于点A,割线PBC分别交圆于点B,C,点D在线段BC上,且DC=2BD,∠BAD=∠PAB,$PA=2\sqrt{10}$,PB=4,则线段AB的长为2$\sqrt{3}$.