题目内容
20.设a,b∈R,则a2(a-b)>0是a>b的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不必要也不充分条件 |
分析 根据不等式的性质,利用充分条件和必要条件的定义进行判断.
解答 解:若(a-b)a2>0,则a≠0且a-b>0,即a>b成立.
当a=0,b=-1时,满足a>b,但(a-b)a2>0不成立,
∴“(a-b)a2>0”是“a>b”的充分不必要条件.
故选:A
点评 本题主要考查充分条件和必要条件的判断,利用不等式的性质是解决本题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
15.若a,b,c均为实数,且ab<0,则下列不等式正确的是( )
| A. | |a+b|>|a-b| | B. | |a|+|b|>|a-b| | C. | |a-c|≤|a-b|+|b-c| | D. | |a-b|<|a|-|b| |
10.四面体ABCD的四个顶点均在半径为2的球面上,若AB、AC、AD两两垂直,$\overrightarrow{BA}•\overrightarrow{BC}$=2,则该四面体体积的最大值为( )
| A. | $\frac{7\sqrt{2}}{6}$ | B. | $\frac{7}{3}$ | C. | 2$\sqrt{2}$ | D. | 7$\sqrt{2}$ |
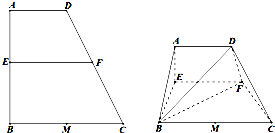 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.