题目内容
7.判断下列函数的奇偶性.(1)f(x)=x2-x3.
(2)f(x)=$\sqrt{{x}^{2}-1}$+$\sqrt{1-{x}^{2}}$
(3)f(x)=$\frac{\sqrt{4-{x}^{2}}}{|x+3|-3}$.
分析 根据函数奇偶性的定义进行判断即可.
解答 解:(1)∵f(-x)=x2+x3.
∴f(-x)≠-f(x),且f(-x)≠f(x),即函数f(x)是非奇非偶函数.
(2)由$\left\{\begin{array}{l}{x^2-1≥0}\\{1-x^2≥0}\end{array}\right.$得$\left\{\begin{array}{l}{x^2≥1}\\{x^2≤1}\end{array}\right.$,即x2=1,解得x=1或x=-1,
定义域为{1,-1},
此时f(x)=0,则f(x)为既是奇函数又是偶函数.
(3)由4-x2≥0得-2≤x≤2,
此时1≤x+3≤5,
即f(x)=$\frac{\sqrt{4-{x}^{2}}}{x+3-3}$=$\frac{\sqrt{4-{x}^{2}}}{x}$,则函数的定义域为{x|-2≤x≤2且x≠0},
则f(-x)=-$\frac{\sqrt{4-{x}^{2}}}{x}$=-f(x),即函数f(x)是奇函数.
点评 本题主要考查函数奇偶性的判断,根据奇偶性的定义是解决本题的关键.注意要先判断定义域是否关于原点对称.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
18.已知集合A={x2-x-2>0},集合B={x||x-a|<3},若A∪B=R,则实数a的取值范围是( )
| A. | [1,2] | B. | (-1,2) | C. | [-1,2] | D. | (-2,1) |
15.若a,b,c均为实数,且ab<0,则下列不等式正确的是( )
| A. | |a+b|>|a-b| | B. | |a|+|b|>|a-b| | C. | |a-c|≤|a-b|+|b-c| | D. | |a-b|<|a|-|b| |
16.执行如图所示的程序框图,若a=1,b=2,则输出的结果是( )
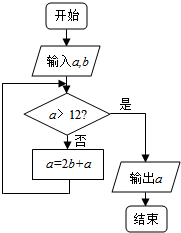

| A. | 9 | B. | 11 | C. | 13 | D. | 15 |
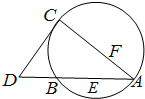 如图,CD为△ABC外接圆的切线,E,F分别为弦AB与弦AC上的点,AB的延长线交直线CD于点D,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,E,F分别为弦AB与弦AC上的点,AB的延长线交直线CD于点D,且BC•AE=DC•AF,B,E,F,C四点共圆.
 如图1,在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,且BC=4,AA${\;}_{1}^{′}$分别交BB1,CC1于点P,Q,将该正方形沿BB1,CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成图2所示的三棱柱ABC-A1B1C1,在图2中:
如图1,在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,且BC=4,AA${\;}_{1}^{′}$分别交BB1,CC1于点P,Q,将该正方形沿BB1,CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成图2所示的三棱柱ABC-A1B1C1,在图2中: