题目内容
1.若函数f(x)=(x2+bx+b)$\sqrt{1-2x}$(b∈R)在区间(0,$\frac{1}{3}$)上单调递增,则b的取值范围为( )| A. | (-∞,$\frac{1}{9}$] | B. | [$\frac{1}{9}$,+∞) | C. | (-∞,$\frac{1}{9}$) | D. | ($\frac{1}{9}$,+∞) |
分析 求出原函数的导函数,由导函数在区间(0,$\frac{1}{3}$)上大于等于0恒成立,得到b≤$\frac{2-5x}{3}$对任意x∈(0,$\frac{1}{3}$)恒成立.由单调性求出$\frac{2-5x}{3}$的范围得答案.
解答 解:由f(x)=(x2+bx+b)$\sqrt{1-2x}$,得:f′(x)=$\frac{-5{x}^{2}-3bx+2x}{\sqrt{1-2x}}$.
由f(x)在区间(0,$\frac{1}{3}$)上单调递增,
得f′(x)≥0对任意x∈(0,$\frac{1}{3}$)恒成立.
即-5x2-3bx+2x≥0对任意x∈(0,$\frac{1}{3}$)恒成立.
∴b≤$\frac{2-5x}{3}$对任意x∈(0,$\frac{1}{3}$)恒成立.
∵$\frac{2-5x}{3}$>$\frac{2-5×\frac{1}{3}}{3}$=$\frac{1}{9}$.
∴b≤$\frac{1}{9}$.
∴b的取值范围是(-∞,$\frac{1}{9}$],
故选:A.
点评 本题考查了利用导数研究函数的单调性,考查了数学转化思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.(普通中学做)如图所示,程序框图输出的某一实数对(x,y)中,若y=32,则x=( )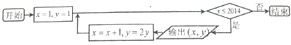
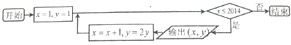
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
 已知正方形ABCD,HG⊥平面ABCD,G,F分别为AB,BC的中点,E为AC上一点,且AE=3EC,求证:EF为异面直线AC与HF的公垂线.
已知正方形ABCD,HG⊥平面ABCD,G,F分别为AB,BC的中点,E为AC上一点,且AE=3EC,求证:EF为异面直线AC与HF的公垂线.