题目内容
13.已知函数$f(x)=\left\{\begin{array}{l}sinx+1,x<2\\{x^2}+bx,x≥2\end{array}\right.$,若$f(f(\frac{π}{2}))=4b$,则b=2.分析 根据函数$f(x)=\left\{\begin{array}{l}sinx+1,x<2\\{x^2}+bx,x≥2\end{array}\right.$,将x=$\frac{π}{2}$代入,构造关于b的方程,解方程可得答案.
解答 解:∵函数$f(x)=\left\{\begin{array}{l}sinx+1,x<2\\{x^2}+bx,x≥2\end{array}\right.$,
∴f(f($\frac{π}{2}$))=f(sin$\frac{π}{2}$+1)=f(2)=4+2b=4b,
解得:b=2,
故答案为:2
点评 本题考查的知识点是函数的值,难度不大,属于基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
1.若函数f(x)=(x2+bx+b)$\sqrt{1-2x}$(b∈R)在区间(0,$\frac{1}{3}$)上单调递增,则b的取值范围为( )
| A. | (-∞,$\frac{1}{9}$] | B. | [$\frac{1}{9}$,+∞) | C. | (-∞,$\frac{1}{9}$) | D. | ($\frac{1}{9}$,+∞) |
8.设数列{an}的前n项和为Sn,令Tn=$\frac{{S}_{1}{+S}_{2}+…+{S}_{n}}{n}$,称Tn为数列a1,a2,…,an的“理想数”,已知数列a1,a2,…,a503的“理想数”为2016,那么数列3,a1,a2,…,a503的理想数是( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
5.在等比数列{an}中,a1,a5是方程x2-12x+9=0的两个实根,则a3为( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 6 |
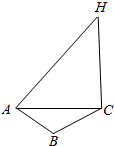 为了测量音乐广场上喷泉的喷射最大高度,小明和小军一个站在A处,一个站在B处,喷泉的喷头在C处,且A、B、C三处位于同一水平面上,A、B两地相距20米,∠BAC=60°,经测量知AC的距离比BC的距离多5m,在A地测得该喷泉射的最高点H的仰角为45°,求该喷泉的最大垂直喷射高度CH.
为了测量音乐广场上喷泉的喷射最大高度,小明和小军一个站在A处,一个站在B处,喷泉的喷头在C处,且A、B、C三处位于同一水平面上,A、B两地相距20米,∠BAC=60°,经测量知AC的距离比BC的距离多5m,在A地测得该喷泉射的最高点H的仰角为45°,求该喷泉的最大垂直喷射高度CH.