题目内容
已知x,y都是正数
(1)若3x+2y=12,求xy的最大值;
(2)若
+
=1,求x+y的最小值.
(1)若3x+2y=12,求xy的最大值;
(2)若
| 4 |
| x |
| 16 |
| y |
(1)∵3x+2y=12,∴xy=
•3x•2y≤
×(
)2=
×36=6,当且仅当3x=2y=6时,等号成立.
∴当且仅当3x=3时,xy取得最大值6.
(2)由x,y∈R+且
+
=1可得,x+y=(x+y)(
+
)=
+
+20≥2
+20=36,
当且仅当
=
,即x=12且y=24时,等号成立,
所以,x+y的最小值是36.
| 1 |
| 6 |
| 1 |
| 6 |
| 3x+2y |
| 2 |
| 1 |
| 6 |
∴当且仅当3x=3时,xy取得最大值6.
(2)由x,y∈R+且
| 4 |
| x |
| 16 |
| y |
| 4 |
| x |
| 16 |
| y |
| 4y |
| x |
| 16x |
| y |
|
当且仅当
| 4y |
| x |
| 16x |
| y |
所以,x+y的最小值是36.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 ,
, 满足线性约束条件
满足线性约束条件 ,则
,则
 的最大值为________.
的最大值为________.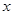 、
、 满足约束条件
满足约束条件 ,则
,则 的最大值等于( )
的最大值等于( )


