题目内容
已知直线ax+by+c-1=0(b、c>0)经过圆x2+y2-2y-5=0的圆心,则
+
的最小值是( )
| 4 |
| b |
| 1 |
| c |
| A.9 | B.8 | C.4 | D.2 |
圆x2+y2-2y-5=0化成标准方程,得x2+(y-1)2=6,
∴圆x2+y2-2y-5=0的圆心为C(0,1),半径r=
.
∵直线ax+by+c-1=0经过圆心C,∴a×0+b×1+c-1=0,即b+c=1,
因此,
+
=(b+c)(
+
)=
+
+5,
∵b、c>0,∴
+
≥2
=4,当且仅当
=
=2时等号成立.
由此可得当b=2c,即b=
且c=
时,
+
=
+
+5的最小值为9.
故选:A
∴圆x2+y2-2y-5=0的圆心为C(0,1),半径r=
| 6 |
∵直线ax+by+c-1=0经过圆心C,∴a×0+b×1+c-1=0,即b+c=1,
因此,
| 4 |
| b |
| 1 |
| c |
| 4 |
| b |
| 1 |
| c |
| 4c |
| b |
| b |
| c |
∵b、c>0,∴
| 4c |
| b |
| b |
| c |
|
| 4c |
| b |
| b |
| c |
由此可得当b=2c,即b=
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| b |
| 1 |
| c |
| 4c |
| b |
| b |
| c |
故选:A

练习册系列答案
相关题目
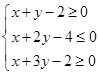 表示的平面区域的面积为________.
表示的平面区域的面积为________.  ,则z=4x+y的最大值为( )
,则z=4x+y的最大值为( ) ,则目标函数
,则目标函数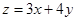 的最大值为 .
的最大值为 . 在直线
在直线 的上方(不含边界),则实数a的取值范围是 .
的上方(不含边界),则实数a的取值范围是 .