Question

【题目】共享单车是指企业在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务，是共享经济的一种新形态，一个共享单车企业在某个城市就“一天中一辆单车的平均成本（单位：元）与租用单车的数量（单位：车辆）之间的关系”进行调查研究，在调查过程中进行了统计，得出相关数据见下表：

租用单车数量（千辆）	2	3	4	5	8
每天一辆车平均成本（元）	3.2	2.4	2	1.9	1.7

根据以上数据，研究人员分别借助甲、乙两种不同的回归模型，得到两个回归方程，方程甲： ，方程乙： .

（1）为了评价两种模型的拟合效果，完成以下任务：

①完成下表（计算结果精确到0.1）（备注： ， 称为相应于点的残差（也叫随机误差））；

租用单车数量（千辆）		2	3	4	5	8
每天一辆车平均成本（元）		3.2	2.4	2	1.9	1.7
模型甲	估计值		2.4	2.1		1.6
	残差		0			0.1
模型乙	估计值		2.3	2	1.9
	残差		0.1	0	0

②分别计算模型甲与模型乙的残差平方和及，并通过比较， 的大小，判断哪个模型拟合效果更好.

（2）这个公司在该城市投放共享单车后，受到广大市民的热烈欢迎，共享单车常常供不应求，于是该公司研究是否增加投放，根据市场调查，这个城市投放8千辆时，该公司平均一辆单一天能收入10元，6元收入的概率分别为0.6，0.4；投放1万辆时，该公司平均一辆单车一天能收入10元，6元收入的概率分别为0.4，0.6，问该公司应该投放8千辆还是1万辆能获得更多利润？（按（1）中拟合效果较好的模型计算一天中一辆单车的平均成本，利润＝收入—成本）.

Answer 1

【答案】(1) 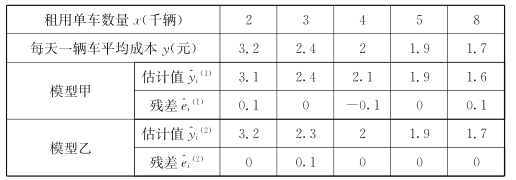， ， ， ，模型乙的拟合效果更好;(2) 投放1万辆能获得更多利润，应该增加到投放1万辆.

【解析】试题分析（1）①通过对回归方程的计算可得两种模型的估计值，代入，即可得残差；②计算可得可知模型乙拟合效果更好；（2）分别计算投放千辆和一万辆时该公司一天获得的总利润，即可得结论。

（1）①经计算，可得下表：

②， ，

，故模型乙的拟合效果更好.

（2）若投放量为8千辆，则公司获得每辆车一天的收入期望为，

所以一天的总利润为（元）

若投放量为1万辆，由（1）可知，每辆车的成本为（元），

每辆车一天收入期望为，

所以一天的总利润为（元）

所以投放1万辆能获得更多利润，应该增加到投放1万辆.