题目内容
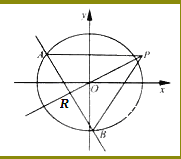
【题目】如图,椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,其左焦点到点
,其左焦点到点![]() 的距离为
的距离为![]() .不过原点O的直线
.不过原点O的直线![]() 与C相交于A,B两点,且线段AB被直线OP平分.
与C相交于A,B两点,且线段AB被直线OP平分.
(1)求椭圆C的方程;
(2)求![]() ABP的面积取最大时直线l的方程.
ABP的面积取最大时直线l的方程.
【答案】(1) ![]() ;(2) 直线l的方程为
;(2) 直线l的方程为![]()
![]() .
.
【解析】试题分析:
(1)由题意可得![]() .则所求椭圆C的方程为:
.则所求椭圆C的方程为: ![]() .
.
(2)首先设出点的坐标,设而不求可得直线AB的斜率为![]() ,然后联立直线与椭圆的方程,结合面积函数,利用导函数研究三角形面积的最大值可得
,然后联立直线与椭圆的方程,结合面积函数,利用导函数研究三角形面积的最大值可得![]() ABP的面积取最大时直线l的方程是
ABP的面积取最大时直线l的方程是![]()
![]() .
.
试题解析:
(1)由题意可得: ![]() ①;
①;
左焦点![]() 到点
到点![]() 的距离为:
的距离为: ![]()
![]() ②.
②.
由①②可解得: ![]() .
.
∴所求椭圆C的方程为: ![]() .
.
(2)易得直线OP的方程: ![]() ,设A(xA,yA),B(xB,yB),R(x0,y0).
,设A(xA,yA),B(xB,yB),R(x0,y0).
其中y0=![]() x0.∵A,B在椭圆上,
x0.∵A,B在椭圆上,
∴ .
.
设直线AB的方程为![]() (m≠0),代入椭圆:
(m≠0),代入椭圆: 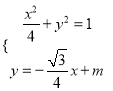 ,
,
整理得: ![]() .
.
显然![]() .
.
∴﹣![]() 且m≠0.由上又有:
且m≠0.由上又有: ![]() ,
, ![]() .
.
∴AB=![]() |
|![]() |=
|=![]()
![]() =
=![]()
![]() .
.
∵点![]() 到直线l的距离表示为:
到直线l的距离表示为: 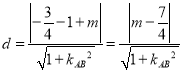 .
.
∴S![]() ABP=
ABP=![]()
![]() =
=![]()
![]() ,
,
令![]() ,
,
则![]() ,
,
﹣![]() 且m≠0,
且m≠0, ![]() ,令
,令![]() 则
则![]() ,
,
解得![]() ,(
,( ![]() ),
),
当![]() 时,
时, ![]()
![]() 递增,
递增,
当![]() 时,
时, ![]()
![]() 递减,
递减,
所以,当且仅当![]() 时,
时, ![]() ABP的面积取最大,
ABP的面积取最大,
此时,直线l的方程为![]()
![]() .
.

【题目】据统计,2016年“双十”天猫总成交金额突破1207亿元.某购物网站为优化营销策略,对11月11日当天在该网站进行网购消费且消费金额不超过1000元的1000名网购者(其中有女性800名,男性200名)进行抽样分析.采用根据性别分层抽样的方法从这1000名网购者中抽取100名进行分析,得到下表:(消费金额单位:元)
女性消费情况:
消费金额 |
|
|
|
|
|
人数 | 5 | 10 | 15 | 47 |
|
男性消费情况:
消费金额 |
|
|
|
|
|
人数 | 2 | 3 | 10 |
| 2 |
(1)计算![]() ,
,![]() 的值;在抽出的100名且消费金额在
的值;在抽出的100名且消费金额在![]() (单位:元)的网购者中随机选出两名发放网购红包,求选出的两名网购者恰好是一男一女的概率;
(单位:元)的网购者中随机选出两名发放网购红包,求选出的两名网购者恰好是一男一女的概率;
(2)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上统计数据填写![]() 列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关?”
列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关?”
女性 | 男性 | 总计 | |
网购达人 | |||
非网购达人 | |||
总计 |
附:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(![]() ,其中
,其中![]() )
)
【题目】共享单车是指企业在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是共享经济的一种新形态,一个共享单车企业在某个城市就“一天中一辆单车的平均成本(单位:元)与租用单车的数量(单位:车辆)之间的关系”进行调查研究,在调查过程中进行了统计,得出相关数据见下表:
租用单车数量 | 2 | 3 | 4 | 5 | 8 |
每天一辆车平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,研究人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ![]() ,方程乙:
,方程乙: ![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务:
①完成下表(计算结果精确到0.1)(备注: ![]() ,
, ![]() 称为相应于点
称为相应于点![]() 的残差(也叫随机误差));
的残差(也叫随机误差));
租用单车数量 | 2 | 3 | 4 | 5 | 8 | |
每天一辆车平均成本 | 3.2 | 2 | 1.9 | 1.7 | ||
模型甲 | 估计值 | 2.4 | 2.1 | 1.6 | ||
残差 | 0 |
| 0.1 | |||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() ,
, ![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(2)这个公司在该城市投放共享单车后,受到广大市民的热烈欢迎,共享单车常常供不应求,于是该公司研究是否增加投放,根据市场调查,这个城市投放8千辆时,该公司平均一辆单一天能收入10元,6元收入的概率分别为0.6,0.4;投放1万辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.4,0.6,问该公司应该投放8千辆还是1万辆能获得更多利润?(按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,利润=收入—成本).