题目内容
设定义域为R的函数f（x）=
，则关于x的方程f2（x）+bf（x）+c=0有5个不同的实数解得充要条件是（ ）
|
| A、b＜0且c＞0 |
| B、b＞0且c＜0 |
| C、b＜0且c=0 |
| D、b≥0且c=0 |
分析：题中原方程f2（x）+af（x）+b=3有且只有5个不同实数解，即要求对应于f（x）=某个常数有3个不同实数解，
故先根据题意作出f（x）的简图：由图可知，只有当f（x）=0时，它有三个根．故关于x的方程f2（x）+af（x）+b=3有且只有5个不同实数解．
故先根据题意作出f（x）的简图：由图可知，只有当f（x）=0时，它有三个根．故关于x的方程f2（x）+af（x）+b=3有且只有5个不同实数解．
解答：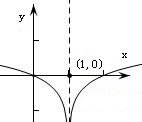
解：∵题中原方程f2（x）+af（x）+b=3有且只有5个不同实数解，
∴即要求对应于f（x）等于某个常数有3个不同实数解，
∴故先根据题意作出f（x）的简图：
由图可知，只有当f（x）=0时，它有三个根．
故关于x的方程f2（x）+af（x）+b=3中c=0，且b＜0．
故选C．
解：∵题中原方程f2（x）+af（x）+b=3有且只有5个不同实数解，∴即要求对应于f（x）等于某个常数有3个不同实数解，
∴故先根据题意作出f（x）的简图：
由图可知，只有当f（x）=0时，它有三个根．
故关于x的方程f2（x）+af（x）+b=3中c=0，且b＜0．
故选C．
点评：数形结合是数学解题中常用的思想方法，能够变抽象思维为形象思维，有助于把握数学问题的本质；另外，由于使用了数形结合的方法，很多问题便迎刃而解，且解法简捷．
练习册系列答案
口算能手系列答案
相关题目