题目内容
【题目】在△ABC中，内角A、B、C所对的边分别为a、b、c，且sinAsinBcosB＋sin2BcosA＝2
sinCcosB.
(1)求tanB的值；
(2)若△ABC的外接圆半径为R，求
的值．
【答案】(1) tanB＝2
. (2)
【解析】
（1）利用两角和差公式对式子sinAsinBcosB＋sin2BcosA＝2sinCcosB进行化简，便可得到结果；
（2）利用同角三角函数关系可得结果.
解：(1)等式sinAsinBcosB＋sin2BcosA＝2sinCcosB化简得，
sinB(sinAcosB＋cosAsinB)＝2sinCcosB，
∴sinBsin(A＋B)＝2sinCcosB，
,
∴sinBsinC＝2sinCcosB，
∵
∴sinC≠0，
∴tanB＝2.
(2)∵tanB＝2，且0<B<π，
∴B为锐角，且
即
，
，
∴
，
解得：cosB＝
.
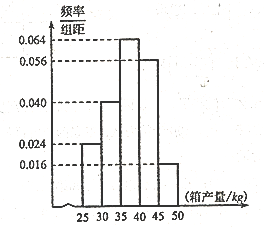
【题目】某书店刚刚上市了《中国古代数学史》，销售前该书店拟定了5种单价进行试销，每种单价（
元）试销l天，得到如表单价（元）与销量
（册）数据：
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
（l）根据表中数据，请建立关于的回归直线方程：
（2）预计今后的销售中，销量（册）与单价（元）服从（l）中的回归方程，已知每册书的成本是12元，书店为了获得最大利润，该册书的单价应定为多少元？
附：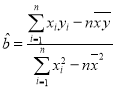
，
，
，
.
【题目】为积极响应国家“阳光体育运动”的号召，某学校在了解到学生的实际运动情况后，发起以“走出教室，走到操场，走到阳光”为口号的课外活动倡议。为调查该校学生每周平均体育运动时间的情况，从高一高二基础年级与高三三个年级学生中按照4:3:3的比例分层抽样，收集300位学生每周平均体育运动时间的样本数据(单位：小时)，得到如图所示的频率分布直方图。
（1）据图估计该校学生每周平均体育运动时间．并估计高一年级每周平均体育运动时间不足4小时的人数；
（2）规定每周平均体育运动时间不少于6小时记为“优秀”，否则为“非优秀”，在样本数据中，有30位高三学生的每周平均体育运动时间不少于6小时，请完成下列
列联表，并判断是否有99%的把握认为“该校学生的每周平均体育运动时间是否“优秀”与年级有关”．
基础年级 | 高三 | 合计 | |
优秀 | |||
非优秀 | |||
合计 | 300 |
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附：K2
，n＝a+b+c+d．
