题目内容
由于某高中建设了新校区,为了交通方便要用三辆通勤车从新校区把教师接到老校区,已知从新校区到老校区有两条公路,汽车走公路①堵车的概率为 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
(1)若三辆汽车中恰有一辆汽车被堵的概率为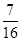 ,求走公路②堵车的概率;
,求走公路②堵车的概率;
(2)在(1)的条件下,求三辆汽车中被堵车辆的个数ξ的分布列和数学期望.
(1) (2)
(2)
解析

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
某工科院校对A,B两个专业的男女生人数进行调查,得到如下的列联表:
| | 专业A | 专业B | 总计 |
| 女生 | 12 | 4 | 16 |
| 男生 | 38 | 46 | 84 |
| 总计 | 50 | 50 | 100 |
(2)能否在犯错误的概率不超过0.05的前提下,认为工科院校中“性别”与“专业”有关系呢?
注:K2=

| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆
| | 轿车A | 轿车B | 轿车C |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
(1)求下表中z的值;
(2)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:94,86,92,96,87,93,90,82把这8辆轿车的得分看作一个总体,从中任取一个得分数
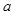 记这8辆轿车的得分的平均数为
记这8辆轿车的得分的平均数为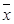 ,定义事件
,定义事件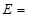 {
{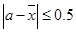 ,且函数
,且函数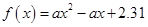 没有零点},求事件
没有零点},求事件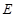 发生的概率
发生的概率  ,乙队获胜的概率为
,乙队获胜的概率为 ,假设每场比赛的结果互相独立.现已赛完两场,乙队以
,假设每场比赛的结果互相独立.现已赛完两场,乙队以 暂时领先.
暂时领先. ,求随机变量
,求随机变量 .
.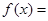
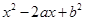 (
(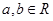 ),若
),若 是从区间
是从区间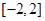 中随机抽取的一个数,
中随机抽取的一个数, 是从区间
是从区间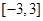 中随机抽取的一个数,求方程
中随机抽取的一个数,求方程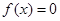 没有实数根的概率.
没有实数根的概率. 的一元二次方程
的一元二次方程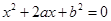 .
. 是从
是从 、
、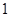 、
、 、
、 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从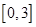 任取的一个数,
任取的一个数,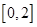 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.