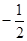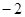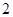题目内容
已知圆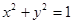 过椭圆
过椭圆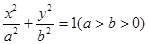 的两焦点,与椭圆有且仅有两个
的两焦点,与椭圆有且仅有两个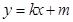 与圆
与圆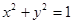 相切 ,与椭圆
相切 ,与椭圆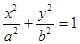 相交于
相交于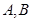 两点记
两点记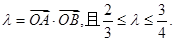
(1)求椭圆的方程
(2)求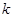 的取值范围;
的取值范围;
(3)求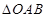 的面积S的取值范围.
的面积S的取值范围.
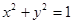 过椭圆
过椭圆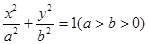 的两焦点,与椭圆有且仅有两个
的两焦点,与椭圆有且仅有两个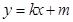 与圆
与圆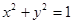 相切 ,与椭圆
相切 ,与椭圆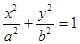 相交于
相交于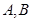 两点记
两点记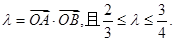
(1)求椭圆的方程
(2)求
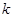 的取值范围;
的取值范围;(3)求
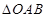 的面积S的取值范围.
的面积S的取值范围.(1)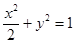 (2)
(2)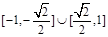 (3)
(3)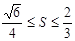
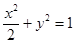 (2)
(2)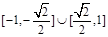 (3)
(3)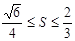
试题分析:(1)由题意可知
 ,方程为
,方程为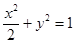 ﹍﹍﹍3分
﹍﹍﹍3分(2)
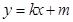 与
与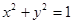 相切,所以原点到直线的距离
相切,所以原点到直线的距离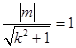
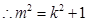 ﹍﹍﹍5分
﹍﹍﹍5分又由
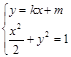 ,(
,(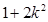 )
)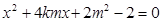
设A(
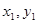 ),B(
),B(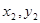 ),则
),则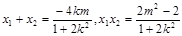 ﹍﹍﹍﹍﹍﹍7分
﹍﹍﹍﹍﹍﹍7分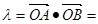
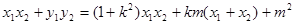
=
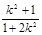 ,由
,由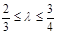 ,故
,故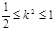 , 即
, 即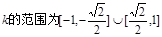 ﹍﹍﹍﹍﹍﹍分
﹍﹍﹍﹍﹍﹍分 (3)
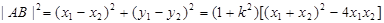
=
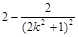 ,由
,由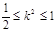 ,得:
,得: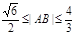 ﹍﹍﹍﹍﹍11分
﹍﹍﹍﹍﹍11分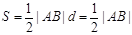 ,所以:
,所以: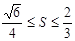 ﹍﹍﹍12分
﹍﹍﹍12分点评:本题第二,三小题难度较大,是能够区别学生能力的题目

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
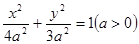 的左焦点为
的左焦点为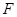 ,直线
,直线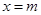 与椭圆相交于点
与椭圆相交于点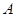 、
、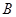 ,当
,当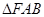 的周长最大时,
的周长最大时,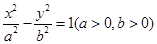 ,过其一个焦点且垂直于实轴的直线与双曲线交于
,过其一个焦点且垂直于实轴的直线与双曲线交于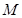 、
、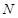 两点,O是坐标原点,满足
两点,O是坐标原点,满足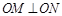 ,则双曲线的离心率为
,则双曲线的离心率为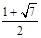
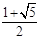
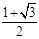
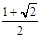
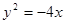 上的焦点
上的焦点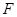 ,点
,点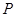 在抛物线上,点
在抛物线上,点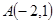 ,则要使
,则要使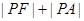 的值最小的点
的值最小的点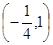
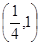
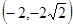
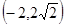
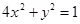 及直线
及直线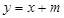 .
.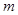 为何值时,直线与椭圆有公共点?
为何值时,直线与椭圆有公共点?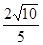 ,求直线的方程.
,求直线的方程.
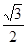

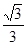
 的离心率
的离心率 ,A,B
,A,B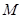 为AB的中点,O为坐标原点,且
为AB的中点,O为坐标原点,且 .
. 交椭圆于P,Q两点,求△POQ面积最大时直线
交椭圆于P,Q两点,求△POQ面积最大时直线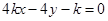 与抛物线
与抛物线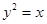 交于
交于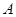 、
、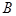 两点,若
两点,若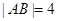 ,则弦
,则弦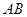 的中点到直线
的中点到直线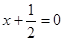 的距离等于( )
的距离等于( )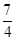
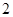
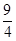
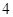
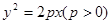 上一定点
上一定点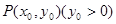 ,作两条直线分别交抛物线于
,作两条直线分别交抛物线于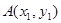 、
、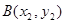 .当
.当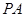 与
与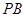 的斜率存在且倾斜角互补时,则
的斜率存在且倾斜角互补时,则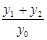 的值为( )
的值为( )