题目内容
16.化简[(a+a-1)2-4]${\;}^{\frac{1}{2}}$-[(a-a-1)2+4]${\;}^{\frac{1}{2}}$=$\frac{-2}{a}$(a>1).分析 由a>1,可得a>a-1.原式变形为$[(a-{a}^{-1})^{2}]^{\frac{1}{2}}$-$[(a+{a}^{-1})^{2}]^{\frac{1}{2}}$,再利用指数幂的运算性质即可得出.
解答 解:∵a>1,∴a>a-1.
原式=$[(a-{a}^{-1})^{2}]^{\frac{1}{2}}$-$[(a+{a}^{-1})^{2}]^{\frac{1}{2}}$
=a-a-1-(a+a-1)
=$\frac{-2}{a}$.
故答案为:$\frac{-2}{a}$.
点评 本题考查了指数幂的运算法则、乘法公式,考查了分类讨论方法、计算能力,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
4.已知函数f(x)=4x2-kx-8在[1,4]上具有单调性,则实数k的取值范围是( )
| A. | (-∞,4]∪[16,+∞) | B. | [4,16] | C. | (-∞,8]∪[32,+∞) | D. | [8,32] |
11.已知函数f(x)=x2+4(a-1)x-3在区间[1,3]上是减函数,则a的取值范围是 ( )
| A. | (-∞,-$\frac{1}{2}$] | B. | (0,$\frac{2}{3}$] | C. | (-∞,$\frac{2}{5}$] | D. | (-∞,1) |
17.已知函数f(x)是R上的减函数,若a∈R,则( )
| A. | f(a)<f(2a) | B. | f(a)<f(-a) | C. | f(a+3)<f(a-2) | D. | f(a)<f(a+1) |
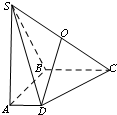 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,点O为侧棱SC的中点,且SA=AB=BC=2,AD=1.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,点O为侧棱SC的中点,且SA=AB=BC=2,AD=1.