题目内容
【题目】如图所示:在五面体ABCDEF中,四边形EDCF是正方形,AD=DE=1,∠ADE=90°,∠ADC=∠DCB=120°.
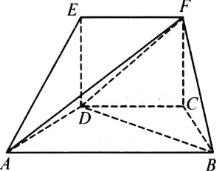
(Ⅰ)求证:平面ABCD⊥平面EDCF;
(Ⅱ)求三棱锥A-BDF的体积.
【答案】(1)见解析:(2)![]()
【解析】
(1)推导出AD⊥DE,CD⊥DE,从而DE⊥平面ABCD,由此能证明平面ABCD⊥平面EDCF,(2)三棱锥A﹣BDF的体积VA﹣BDF=VF﹣ABD![]() ,由此能求出结果.
,由此能求出结果.
(1)证明:∵在五面体ABCDEF中,四边形EDCF是正方形,∠ADE=90°,
∴AD⊥DE,CD⊥DE,
∵AD∩CD=D,∴DE⊥平面ABCD,
∵DE平面EDCF,∴平面ABCD⊥平面EDCF.
(2) 由(1)知DE⊥平面![]() ,所以
,所以![]() 平面
平面![]() . 等腰三角形
. 等腰三角形![]()
又DC∥EF,![]() 平面ABFE,
平面ABFE,![]() 平面ABFE,所以DC∥平面ABFE.
平面ABFE,所以DC∥平面ABFE.
又平面ABCD∩平面ABFE=AB,故AB∥CD.所以四边形![]() 为等腰梯形.又AD=DE,所以AD=CD=CB,由
为等腰梯形.又AD=DE,所以AD=CD=CB,由![]() ,在等腰
,在等腰![]() 中由余弦定理得BD=
中由余弦定理得BD=![]() ,
,![]() AD
AD![]() BD,所以三棱锥
BD,所以三棱锥![]() 的体积为
的体积为![]() .
.

练习册系列答案
相关题目
【题目】在万众创新的大经济背景下,某成都青年面包店推出一款新面包,每个面包的成本价为![]() 元,售价为
元,售价为![]() 元,该款面包当天只出一炉(一炉至少
元,该款面包当天只出一炉(一炉至少![]() 个,至多
个,至多![]() 个),当天如果没有售完,剩余的面包以每个
个),当天如果没有售完,剩余的面包以每个![]() 元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近
元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近![]() 天的日需求量(单位:个),整理得下表:
天的日需求量(单位:个),整理得下表:
日需求量 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)以![]() 天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为
天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为![]() ,记当日这款新面包获得的总利润为
,记当日这款新面包获得的总利润为![]() (单位:元).求
(单位:元).求![]() 的分布列及其数学期望.
的分布列及其数学期望.
相关公式: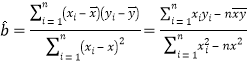 ,
,![]()

