题目内容
【题目】已知函数f(x)=(kx+![]() )ex﹣2x,若f(x)<0的解集中有且只有一个正整数,则实数k的取值范围为 ( )
)ex﹣2x,若f(x)<0的解集中有且只有一个正整数,则实数k的取值范围为 ( )
A. [![]() ,
,![]() )B. (
)B. (![]() ,
,![]() ]
]
C. [![]() )D. [
)D. [![]() )
)
【答案】A
【解析】
把f(x)<0转化为(kx+![]() )ex<2x,即kx+
)ex<2x,即kx+![]() <
<![]() ,令g(x)=
,令g(x)=![]() ,利用导数研究g(x)的单调性,数形结合得答案.
,利用导数研究g(x)的单调性,数形结合得答案.
由f(x)<0,得(kx+![]() )ex<2x,即kx+
)ex<2x,即kx+![]() <
<![]() ,令g(x)=
,令g(x)=![]() ,则g′(x)=
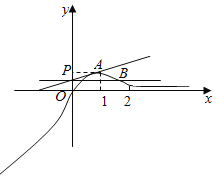
,则g′(x)=![]() ,当x∈(﹣∞,1)时,g′(x)>0,当x∈(1,+∞)时,g′(x)<0.∴g(x)在(﹣∞,1)上单调递增,在(1,+∞)上单调递减.作出函数g(x)与y=kx+
,当x∈(﹣∞,1)时,g′(x)>0,当x∈(1,+∞)时,g′(x)<0.∴g(x)在(﹣∞,1)上单调递增,在(1,+∞)上单调递减.作出函数g(x)与y=kx+![]() 的图象如图:y=kx+
的图象如图:y=kx+![]() 的图象过定点P(0,
的图象过定点P(0,![]() ),A(1,
),A(1,![]() ),B(2,
),B(2,![]() ),∵
),∵![]() ,
,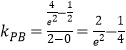 .∴实数k的取值范围为[
.∴实数k的取值范围为[![]() ,
,![]() ).
).
故选:A.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目