题目内容
18.设a是实数,g(x)是指数函数,且g(x)的图象过点(2,4),若f(x)=a-$\frac{2}{g(x)+1}$(x∈R).(1)试证明:对于任意的a,f(x)在R上为增函数;
(2)试确定a的值,使f(x)为奇函数.
分析 (1)设g(x)=mx,把点(2,4)代入求出g(x)和f(x),利用函数的单调性定义、指数函数的单调性证明结论即可;
(2)由f(x)是R上奇函数、奇函数的定义得:f(0)=0,列出方程求出a的值.
解答 证明:(1)设g(x)=mx(m>0且m≠1),
因为g(x)的图象过点(2,4),
所以m2=4,解得m=2,则g(x)=2x,
即$f(x)=a-\frac{2}{{2}^{x}+1}$,
设设x1、x2∈R且x1<x2,
f(x1)-f(x2)=($a-\frac{2}{{2}^{{x}_{1}}+1}$)-($a-\frac{2}{{2}^{{x}_{2}}+1}$)
=$-\frac{2}{{2}^{{x}_{1}}+1}+\frac{2}{{2}^{{x}_{2}}+1}$=$\frac{-2({2}^{{x}_{2}}+1)+2({2}^{{x}_{1}}+1)}{{(2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$
=$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{{(2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$
又由y=2x在R上为增函数,且x1<x2,
则${2}^{{x}_{1}}>0$,${2}^{{x}_{2}}>0$,${2}^{{x}_{1}}<{2}^{{x}_{2}}$,
所以$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{{(2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}<0$,则f(x1)-f(x2)<0,
即f(x1)<f(x2),
所以对于任意的a,f(x)在R上为增函数;
解:(2))若f(x)为奇函数,且其定义域为R,
必有f(0)=0,则$a-\frac{2}{{2}^{0}+1}$=0,解得a=1,
当a=1时,f(x)为奇函数.
点评 本题考查函数奇偶性的应用,函数单调性的证明,指数函数的单调性,考查化简、变形能力,属于中档题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| 每户丢弃旧塑料袋个数 | 2 | 3 | 4 | 5 |
| 户数 | 10 | 10 | 20 | 10 |
(2)求这50户居民每天丢弃旧塑料袋的方差.
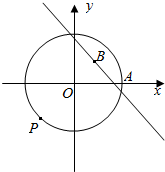 点A(2,0)是圆x2+y2=4上的定点,点B(1,1)是圆内一点,P为圆上的动点.
点A(2,0)是圆x2+y2=4上的定点,点B(1,1)是圆内一点,P为圆上的动点.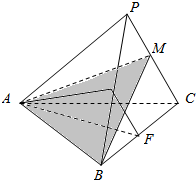 在三棱锥P-ABC中,AP=AC,BP=BC,E、F、M分别是PB、BC、CP的中点,求证:平面AEF⊥平面ABM.
在三棱锥P-ABC中,AP=AC,BP=BC,E、F、M分别是PB、BC、CP的中点,求证:平面AEF⊥平面ABM.