题目内容

9．设x∈R，则“|x-2|＜1”是“x2+x＞0”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

分析 根据充分条件和必要条件的定义进行判断即可．

解答 解：由|x-2|＜1得-1＜x-2＜1，得1＜x＜3，
由x2+x＞0得x＞0或x＜-1，
则“|x-2|＜1”是“x2+x＞0”的充分不必要条件，
故选：A

点评 本题主要考查充分条件和必要条件的判断，根据不等式的解法求出不等式的等价条件是解决本题的关键．

练习册系列答案
相关题目
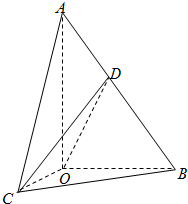19．如图，在Rt△AOB中，∠OAB=$\frac{π}{6}$，斜边AB=4．Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到，且二面角B-AO-C是直二面角，动点D在斜边AB上．
（Ⅰ）求证：平面COD⊥平面AOB；
（Ⅱ）求CD与平面AOB所成角的正弦的最大值．
20．函数f（x）=4cos2$\frac{x}{2}$cos（$\frac{π}{2}$-x）-2sinx-|ln（x+1）|的零点个数为（　　）
A．1B．2C．3D．4
17．椭圆$\frac{{x}^{2}}{4}$+y2=1的长轴长为（　　）
A．4B．2C．1D．2$\sqrt{3}$
4．已知f（x）=3x4+2x3+x-3，用秦九韶算法求当x=2时v2=16的值．
14．设$\overrightarrow{a}，\overrightarrow{b}$是两个非零的平面向量，给出下列说法
①若$\overrightarrow{a}•\overrightarrow{b}$=0，则有$|\overrightarrow{a}+\overrightarrow{b|}=|\overrightarrow{a}-\overrightarrow{b}|$；②$|\overrightarrow{a}•\overrightarrow{b}|=|\overrightarrow{a}||\overrightarrow{b}|$；③若存在实数λ，使$\overrightarrow{a}=λ\overline{b}$，则$|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a|}+|\overrightarrow{b}|$；④若$|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}|+|\overrightarrow{b|}$，则存在实数λ，使得$\overrightarrow{a}=λ\overrightarrow{b}$．其中说法正确的个数是（　　）
A．1B．2C．3D．4
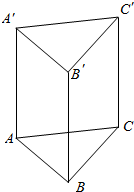1．如图，已知$\overrightarrow{AA'}$=$\overrightarrow{BB'}$=$\overrightarrow{CC'}$，求证：
（1）△ABC≌△A′B′C′；
（2）$\overrightarrow{AB}$=$\overrightarrow{A'B'}$，$\overrightarrow{AC}$=$\overrightarrow{A'C'}$．
18．设a是实数，g（x）是指数函数，且g（x）的图象过点（2，4），若f（x）=a-$\frac{2}{g（x）+1}$（x∈R）．
（1）试证明：对于任意的a，f（x）在R上为增函数；
（2）试确定a的值，使f（x）为奇函数．
19．已知a，b，c分别是△ABC的三个内角A，B，C所对的边，若△ABC的面积S=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{4}$，则角C的大小是（　　）
A．90°B．60°C．45°D．30°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网