��Ŀ����
20����֪ƽ��ֱ������ϵxoy�У���OΪ���㣬x���������Ϊ���ᣬ����������ϵ������C1����Ϊ��=2sin�ȣ�C2�IJ�������Ϊ$\left\{\begin{array}{l}x=-1+\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$��tΪ������������д������C1��ֱ�����귽�̺�C2����ͨ���̣�
�������PΪ����C1�ϵ�����һ�㣬���P ������C2�����ȡֵ��Χ��
���� ��I��ֱ�����ü�������ֱ�����껥�����C1��ֱ�����귽�̣�C2����ͨ���̣�
��II�����C1Ϊ�ԣ�0��1��ΪԲ�ģ�r=1Ϊ�뾶��Բ������Բ�ľ��Ƴ��������ֵ�õ���Χ���ɣ�
��� ����С������10�֣�
�⣺��I������C1����Ϊ��=2sin�ȣ��ɵæ�2=2��sin�ȣ��ɵ�x2+y2=2y��
��C1��ֱ�����귽�̣�x2+��y-1��2=1��
C2�IJ�������Ϊ$\left\{\begin{array}{l}x=-1+\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$����ȥ����t�ɵã�
C2����ͨ���̣�$\sqrt{3}x-y+\sqrt{3}=0$������4�֣�
��II���ɣ�I��֪��C1Ϊ�ԣ�0��1��ΪԲ�ģ�r=1Ϊ�뾶��Բ��C1��Բ�ģ�0��1����C2�ľ���Ϊ$d=\frac{{|{-1+\sqrt{3}}|}}{{\sqrt{3+1}}}=\frac{{\sqrt{3}-1}}{2}��1$����C1��C2�ཻ��P������C2������СֵΪ0�����ֵΪ$d+r=\frac{{\sqrt{3}+1}}{2}$��
���P������C2�����ȡֵ��ΧΪ$[{0��\frac{{\sqrt{3}+1}}{2}}]$������10�֣�
���� ���⿼�鼫������ֱ�����귽�̵Ļ���������������ֱ�����귽�̵Ļ������������������

��ϰ��ϵ�д�
 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
�����Ŀ
11����֪����{an}�У�a2=102��an+1-an=4n��������$\left\{{\frac{a_n}{n}}\right\}$����С���ǣ�������
| A�� | ��6�� | B�� | ��7�� | C�� | ��8�� | D�� | ��9�� |
5������|x|+|y|=1��ʾ�������ǣ�������
| A�� |  | B�� | 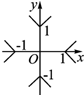 | C�� |  | D�� |  |
12��������A={x|-1��x��2}��B={x|��2x+1����3-x����0}����A��B�ǣ�������
| A�� | {x|2��x��3} | B�� | {x|-$\frac{1}{2}$��x��2} | C�� | {x|-1$��x��-\frac{1}{2}$} | D�� | {x|-1$��x��\frac{1}{2}$��2��x��3} |