题目内容
已知二次函数 满足条件
满足条件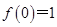 和
和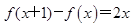 .
.
(1)求 ;
;
(2)求 在区间
在区间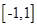 上的最大值和最小值.
上的最大值和最小值.
(1)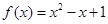 ;(2)
;(2) 在区间
在区间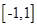 上的最大值为
上的最大值为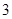 ,最小值为
,最小值为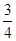 .
.
解析试题分析:(1)先设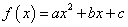 ,用待定系数法求出
,用待定系数法求出 ;
;
(2)由(1)知函数开口向上,对称轴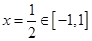 ,结合单调性可求出函数
,结合单调性可求出函数 在区间
在区间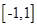 上的最大值和最小值.
上的最大值和最小值.
(1)设二次函数表达式为: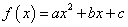 ,由已知可得:
,由已知可得: ,
,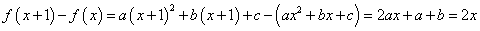
则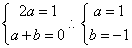 ,
,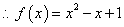
(2)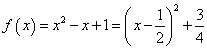 ,则当
,则当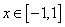 时,
时,
考点:解析式的求法、函数的最值.

练习册系列答案
相关题目
题目内容
已知二次函数 满足条件
满足条件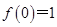 和
和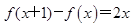 .
.
(1)求 ;
;
(2)求 在区间
在区间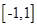 上的最大值和最小值.
上的最大值和最小值.
(1)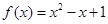 ;(2)
;(2) 在区间
在区间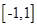 上的最大值为
上的最大值为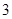 ,最小值为
,最小值为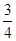 .
.
解析试题分析:(1)先设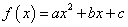 ,用待定系数法求出
,用待定系数法求出 ;
;
(2)由(1)知函数开口向上,对称轴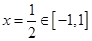 ,结合单调性可求出函数
,结合单调性可求出函数 在区间
在区间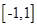 上的最大值和最小值.
上的最大值和最小值.
(1)设二次函数表达式为: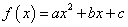 ,由已知可得:
,由已知可得: ,
,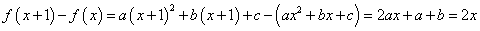
则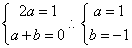 ,
,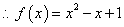
(2)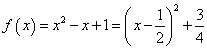 ,则当
,则当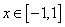 时,
时,
考点:解析式的求法、函数的最值.
