题目内容
【题目】已知函数f(x)=2lnx+x2+(a﹣1)x﹣a,(a∈R),当x≥1时,f(x)≥0恒成立.
(1)求实数a的取值范围;
(2)若正实数x1、x2(x1≠x2)满足f(x1)+f(x2)=0,证明:x1+x2>2.
【答案】
(1)解: ![]()
当a≥﹣3时, ![]() ,f(1)=0.
,f(1)=0.
∴当x≥1时,f(x)≥0成立.
当a<﹣3时,存在大于1的实数m,使得f'(m)=0
∴当1<x<m时,f'(x)<0成立.
∴f(x)在区间(1,m)上单调递减;
∴当1<x<m时,f(x)<f(1)=0;
∴a<﹣3不可能成立.
所以a≥﹣3.
(2)解:不妨设x1<x2
∵正实数x1、x2满足f(x1)+f(x2)=0,
有(1)可知,0<x1<1<x2;
又∵f(x)为单调递增函数,
所以x1+x2>2x2>2﹣x1f(x2)>f(2﹣x1)
又∵f(x1)+f(x2)=0f(x2)=﹣f(x1)
所以只要证明:﹣f(x1)>f(2﹣x1)f(x1)+f(2﹣x1)<0
设g(x)=f(x)+f(2﹣x)则g(x)=2[lnx+ln(2﹣x)+x2﹣2x+1],
可得 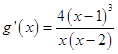
∴当0<x<1时,g'(x)>0成立
∴g(x)在区间(0,1)上单调增函数.
又∵g(1)=0
∴当0<x<1时,g(x)<0成立,即f(x)+f(2﹣x)<0.
所以不等式f(x1)+f(2﹣x1)<0成立.
所以x1+x2>2.
【解析】(1)求出导函数,通过当a≥﹣3时,当a<﹣3时,利用函数的单调性,转化求解a≥﹣3.(2)不妨设x1<x2推出f(x1)+f(x2)=0f(x2)=﹣f(x1),只要证明:﹣f(x1)>f(2﹣x1)f(x1)+f(2﹣x1)<0,设g(x)=f(x)+f(2﹣x)求出 ![]() ,利用函数的单调性转化证明即可.
,利用函数的单调性转化证明即可.

练习册系列答案
相关题目