题目内容
【题目】如图,已知AB是半径为2的半球O的直径,P,D为球面上的两点且∠DAB=∠PAB=60°, ![]() .
. 
(1)求证:平面PAB⊥平面DAB;
(2)求二面角B﹣AP﹣D的余弦值.
【答案】
(1)证明:在△PAB中,过P作PH⊥AB于点H,连HD.
由Rt△APB≌Rt△ADB可知DH⊥AB,且 ![]() ,
,
又 PH2+HD2=3+3=6=PD2,∴PH⊥HD.
又AB∩HD=H,∴PH⊥平面ABD,又PH平面PAB,
∴平面PAB⊥平面ABD.
(2)解:由(1)可知HB,HD,HP两两垂直,
故以H为原点,HB,HD,HP所在直线分别为x轴,y轴,z轴,如图建立空间直角坐标系,可知 ![]() .
.
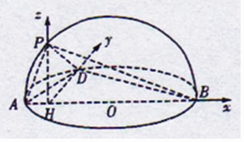
设平面APD的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 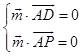 ,即
,即 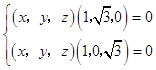 ,
,
∴ 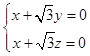 ,
,
令 ![]() ,则得y=z=1,∴
,则得y=z=1,∴ ![]() ,
,
又平面APB的法向量 ![]() =(0,1,0),
=(0,1,0),
∴cos ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
而二面角B﹣AP﹣D与m,n的夹角相等,
因此所求的二面角B﹣AP﹣D的余弦值为 ![]() .
.
【解析】(1)在△PAB中,过P作PH⊥AB于点H,连HD.证明DH⊥AB,PH⊥HD.推出PH⊥平面ABD,然后证明平面PAB⊥平面ABD.(2)由(1)可知HB,HD,HP两两垂直,故以H为原点,HB,HD,HP所在直线分别为x轴,y轴,z轴,求出相关点的坐标求出平面APD的法向量,平面APB的法向量,利用空间向量的数量积求解二面角B﹣AP﹣D的余弦值即可.
【考点精析】通过灵活运用平面与平面垂直的判定,掌握一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




