题目内容
设f(x)是定义在R上的奇函数,且满足f(x+2)=-f(x);又当0≤x≤1时,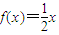 ,则方程
,则方程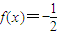 的解集为 .
的解集为 .
【答案】分析:先根据f(x)是奇函数且f(x+2)=-f(x)求出函数的周期性,以及-1≤x≤0时的解析式,然后求出在[-1,1]上满足方程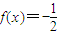 的解,最后根据周期性即可求出所求.
的解,最后根据周期性即可求出所求.
解答:解:∵f(x)是奇函数且f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x)则T=4
∵当0≤x≤1时,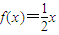 ,f(x)是奇函数
,f(x)是奇函数
∴当-1≤x≤0时,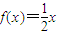 ,
,
令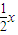 =-
=- 解得:x=-1
解得:x=-1
而函数f(x)是以4为周期的周期函数
∴方程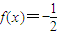 的解集为{x|x=4k-1,k∈Z}
的解集为{x|x=4k-1,k∈Z}
故答案为:{x|x=4k-1,k∈Z}
点评:本题主要考查函数的奇偶性和递推关系,这类题往往是奇偶性和周期性结合来转化求值区间,属于基础题.
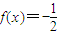 的解,最后根据周期性即可求出所求.
的解,最后根据周期性即可求出所求.解答:解:∵f(x)是奇函数且f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x)则T=4
∵当0≤x≤1时,
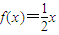 ,f(x)是奇函数
,f(x)是奇函数∴当-1≤x≤0时,
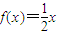 ,
,令
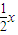 =-
=- 解得:x=-1
解得:x=-1而函数f(x)是以4为周期的周期函数
∴方程
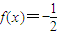 的解集为{x|x=4k-1,k∈Z}
的解集为{x|x=4k-1,k∈Z}故答案为:{x|x=4k-1,k∈Z}
点评:本题主要考查函数的奇偶性和递推关系,这类题往往是奇偶性和周期性结合来转化求值区间,属于基础题.

练习册系列答案
相关题目
设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2+a(a是常数).则x∈[2,4]时的解析式为( )
| A、f(x)=-x2+6x-8 | B、f(x)=x2-10x+24 | C、f(x)=x2-6x+8 | D、f(x)=x2-6x+8+a |