题目内容
设f(x)是定义在R上的奇函数,且f(1)=0,当x>0时,有f(x)>xf′(x)恒成立,则不等式xf(x)>0的解集为( )
分析:由已知当x>0时总有xf′(x)<f(x)成立,可判断函数g(x)=
为减函数,由f(x)是定义在R上的奇函数,可得g(x)为(-∞,0)∪(0,+∞)上的偶函数,根据函数g(x)在(0,+∞)上的单调性和奇偶性,结合g(x)的图象,解不等式即可
| f(x) |
| x |
解答:解:设g(x)=
则g(x)的导数为g′(x)=
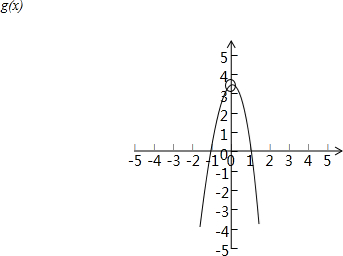
∵当x>0时总有xf′(x)<f(x)成立,即当x>0时,g′(x)<0,
∴当x>0时,函数g(x)=
为减函数,
又∵g(-x)=
=
=g(x)
∴函数g(x)为定义域上的偶函数
又∵g(1)=
=0
∴函数g(x)的图象如图:数形结合可得
∵xf(x)>0且,f(x)=xg(x)(x≠0)
∴x2•g(x)>0
∴g(x)>0
∴0<x<1或-1<x<0
故选D
| f(x) |
| x |
则g(x)的导数为g′(x)=
| xf,(x)-f(x) |
| x2 |
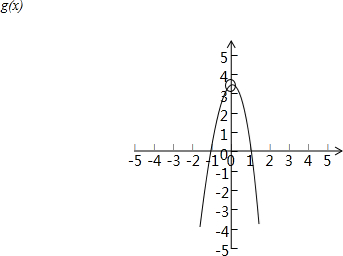
∵当x>0时总有xf′(x)<f(x)成立,即当x>0时,g′(x)<0,
∴当x>0时,函数g(x)=
| f(x) |
| x |
又∵g(-x)=
| f(-x) |
| -x |
| f(x) |
| x |
∴函数g(x)为定义域上的偶函数
又∵g(1)=
| f(1) |
| 1 |
∴函数g(x)的图象如图:数形结合可得
∵xf(x)>0且,f(x)=xg(x)(x≠0)
∴x2•g(x)>0
∴g(x)>0
∴0<x<1或-1<x<0
故选D
点评:本题主要考查了利用导数判断函数的单调性,并由函数的奇偶性和单调性解不等式,属于综合题.

练习册系列答案
相关题目
设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2+a(a是常数).则x∈[2,4]时的解析式为( )
| A、f(x)=-x2+6x-8 | B、f(x)=x2-10x+24 | C、f(x)=x2-6x+8 | D、f(x)=x2-6x+8+a |