题目内容
已知数列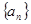 的前
的前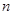 项和为
项和为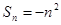 ,则( )
,则( )
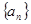 的前
的前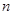 项和为
项和为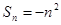 ,则( )
,则( )A.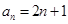 | B.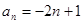 |
C.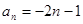 | D.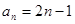 |
B
分析:根据数列{an}的前n项和Sn,表示出数列{an}的前n-1项和Sn-1,两式相减即可求出此数列的通项公式,然后把n=1代入也满足,故此数列为等差数列,求出的an即为通项公式,
解答:解:当n=1时,S1=-12=-1,
当n≥2时,an=Sn-Sn-1=-n2+(n-1)2=-2n+1,
又n=1时,a1=-2+1=-1,满足通项公式,
∴此数列为等差数列,其通项公式为an=-2n+1,
故选B.
点评:此题考查了等差数列的通项公式,灵活运用an=Sn-Sn-1求出数列的通项公式是解本题的关键.
解答:解:当n=1时,S1=-12=-1,
当n≥2时,an=Sn-Sn-1=-n2+(n-1)2=-2n+1,
又n=1时,a1=-2+1=-1,满足通项公式,
∴此数列为等差数列,其通项公式为an=-2n+1,
故选B.
点评:此题考查了等差数列的通项公式,灵活运用an=Sn-Sn-1求出数列的通项公式是解本题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
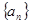 和
和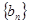 ,若对任意正整数
,若对任意正整数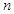 ,恒有
,恒有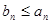 ,则称数列
,则称数列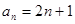 ,请写出一个公比不为1的等比数列
,请写出一个公比不为1的等比数列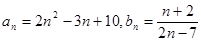 ,求证数列
,求证数列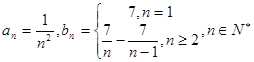 ,构造
,构造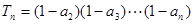 ,
,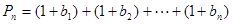 ,求使
,求使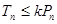 对
对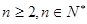 恒成立的
恒成立的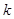 的最小值.
的最小值.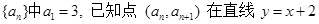 上,
上,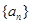 的通项公式; (2)若
的通项公式; (2)若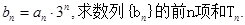
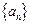 中,
中,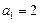 ,前
,前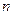 项和为
项和为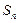 ,若数列
,若数列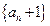 也是等比数列,则
也是等比数列,则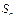 等于( )
等于( )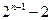
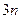
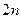
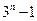
 ;
;
 (1)求 ;(2) 求证: 为等比数列;(3)求玩该游戏获胜的概率。
(1)求 ;(2) 求证: 为等比数列;(3)求玩该游戏获胜的概率。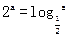 ,
,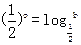 ,
,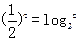 ,则a、b、c从小到大的顺序是_________________.
,则a、b、c从小到大的顺序是_________________.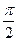 ),且cosa=a,sin(cosb)=b,cos(sinc)=c,则a、b、c从小到大的顺序是_____________
),且cosa=a,sin(cosb)=b,cos(sinc)=c,则a、b、c从小到大的顺序是_____________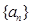 的前n项和为
的前n项和为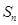 ,若
,若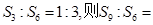 ( )
( )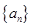 的前
的前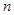 项和为
项和为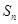 ,
,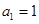 ,当
,当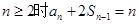 ,则
,则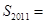 ;
;