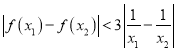题目内容
【题目】质检部门对某工厂甲、乙两个车间生产的12个零件质量进行检测．甲、乙两个车间的零件质量(单位：克)分布的茎叶图如图所示．零件质量不超过20克的为合格．
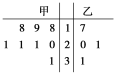
（1）从甲、乙两车间分别随机抽取2个零件，求甲车间至少一个零件合格且乙车间至少一个零件合格的概率；
（2）质检部门从甲车间8个零件中随机抽取3个零件进行检测，已知三件中有两件是合格品的条件下，另外一件是不合格品的概率．
（3）若从甲、乙两车间12个零件中随机抽取2个零件，用
表示乙车间的零件个数，求X的分布列与数学期望．
【答案】（1）
（2）
（3）见解析，
【解析】
（1）考虑甲、乙两车间抽取的
个零件都不合格的情况，利用对立事件的概率求解方法即可计算出目标事件的概率；
（2）先考虑抽取的
个零件中至少有个是合格的取法数，再考虑抽取的个零件中个合格
个不合格的取法数，根据古典概型的概率计算公式计算出目标事件的概率；
（3）先列出
的可取值并计算出对应取值的概率，然后即可得到的分布列并计算出数学期望.
（1）由题意得甲车间的合格零件数为4，乙车间的合格零件数为2，
故所求概率为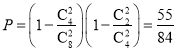
．
即甲车间至少一个零件合格且乙车间至少一个零件合格的概率为．
（2）因为抽取的个零件中至少有个是合格的取法数有：
种，
抽取的个零件中个合格个不合格的取法数有：
种，
所以三件中有两件是合格品的条件下，另外一件是不合格品的概率：
；
(3)由题意可得的所有可能取值为0，1，2．
，
，
．
∴ 随机变量的分布列为
| 0 | 1 | 2 |
|
|
|
|
．
练习册系列答案
相关题目
