题目内容
【题目】某地区2020年清明节前后3天每天下雨的概率为60%，通过模拟实验的方法来计算该地区这3天中恰好有2天下雨的概率：用随机数
（
，且
）表示是否下雨：当
时表示该地区下雨，当
时，表示该地区不下雨，从随机数表中随机取得20组数如下
332 714 740 945 593 468 491 272 073 445
992 772 951 431 169 332 435 027 898 719
（1）求出
的值，并根据上述数表求出该地区清明节前后3天中恰好有2天下雨的概率；
（2）从2011年开始到2019年该地区清明节当天降雨量（单位：
）如下表：（其中降雨量为0表示没有下雨）.
时间 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
降雨量 | 29 | 28 | 26 | 27 | 25 | 23 | 24 | 22 | 21 |
经研究表明：从2011年开始至2020年， 该地区清明节有降雨的年份的降雨量
与年份
成线性回归，求回归直线
，并计算如果该地区2020年（
）清明节有降雨的话，降雨量为多少？（精确到0.01）
参考公式：
.
参考数据：
，
，
，
.
【答案】（1）
，概率为
；（2）回归直线方程为：
，2020年清明节有降雨的话，降雨量约为
．
【解析】
（1）根据每天下雨概率可求得
，在所给20组数确定表示3天中恰有2天下雨的组数，然后计算概率；
（2）计算
，根据所给数据求出回归直线方程中的系数，得回归直线方程，令
可得2020年的预估值．
（1）由
得，即
表示下雨，
表示不下雨，
所给20组数中有714，740，945，593，491，272，073，951，169，027共10组表示3天中恰有两天下雨，∴所求概率为
.
（2）由所给数据得
，
，
，
，
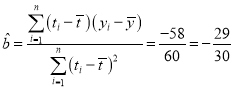∴回归直线方程为：，
时，
，
∴2020年清明节有降雨的话，降雨量约为．
数学奥赛暑假天天练南京大学出版社系列答案
【题目】进入12月以来，某地区为了防止出现重污染天气，坚持保民生、保蓝天，严格落实机动车限行等一系列“管控令”，该地区交通管理部门为了了解市民对“单双号限行”的赞同情况，随机采访了220名市民，将他们的意见和是否拥有私家车情况进行了统计，得到如下的2×2列联表：
| 赞同限行 | 不赞同限行 | 合计 |
没有私家车 | 90 | 20 | 110 |
有私家车 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
（1）根据上面的列联表判断，能否有99%的把握认为“赞同限行与是否拥有私家车”有关；
（2）为了解限行之后是否对交通拥堵、环境污染起到改善作用，从上述调查的不赞同限行的人员中按分层抽样抽取6人，再从这6人中随机抽出2名进行电话回访，求抽到的2人中至少有1名“没有私家车”人员的概率．
参考公式：K2＝
P（K2≥k） | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3..841 | 6.635 | 7.879 | 10.828 |
