题目内容
11.已知数列{an}与{bn}满足an+1-an=2(bn+1-bn),n∈N*.(1)若bn=3n+5,且a1=1,求{an}的通项公式;
(2)设{an}的第n0项是最大项,即an0≥an(n∈N*),求证:{bn}的第n0项是最大项;
(3)设a1=3λ<0,bn=λn(n∈N*),求λ的取值范围,使得对任意m,n∈N*,an≠0,且$\frac{a_m}{a_n}∈({\frac{1}{6},6})$.
分析 (1)把bn=3n+5代入已知递推式可得an+1-an=6,由此得到{an}是等差数列,则an可求;
(2)由an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1,结合递推式累加得到an=2bn+a1-2b1,求得${b}_{n}=\frac{1}{2}({a}_{n}+2{b}_{1}-{a}_{1})$,进一步得到
${b}_{{n}_{0}}=\frac{1}{2}({a}_{{n}_{0}}+2{b}_{1}-{a}_{1})≥\frac{1}{2}({a}_{n}+2{b}_{1}-{a}_{1})$得答案;
(3)由(2)可得${a}_{n}=2{λ}^{n}+λ$,然后分-1<λ<0,λ=-1,λ<-1三种情况求得an的最大值M和最小值m,再由$\frac{M}{m}$∈($\frac{1}{6},6$)列式求得λ的范围.
解答 (1)解:∵an+1-an=2(bn+1-bn),bn=3n+5,
∴an+1-an=2(bn+1-bn)=2(3n+8-3n-5)=6,
∴{an}是等差数列,首项为a1=1,公差为6,
则an=1+(n-1)×6=6n-5;
(2)∵an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2(bn-bn-1)+2(bn-1-bn-2)+…+2(b2-b1)+a1
=2bn+a1-2b1,
∴${b}_{n}=\frac{1}{2}({a}_{n}+2{b}_{1}-{a}_{1})$,
∴${b}_{{n}_{0}}=\frac{1}{2}({a}_{{n}_{0}}+2{b}_{1}-{a}_{1})≥\frac{1}{2}({a}_{n}+2{b}_{1}-{a}_{1})$.
∴数列{bn}的第n0项是最大项;
(3)由(2)可得${a}_{n}=2{λ}^{n}+λ$,
①当-1<λ<0时,${a}_{2n}=2({λ}^{2})^{n}+λ$单调递减,有最大值$M={a}_{2}=2{λ}^{2}+λ$;
${a}_{2n-1}=2{λ}^{2n-1}+λ$单调递增,有最小值m=a1=3λ<0,
∴$\frac{{a}_{m}}{{a}_{n}}$的最小值为$\frac{M}{m}=\frac{2λ+1}{3}$,最大值为$\frac{m}{M}=\frac{3}{2λ+1}$,
则$\left\{\begin{array}{l}{\frac{2λ+1}{3}>\frac{1}{6}}\\{\frac{3}{2λ+1}<6}\end{array}\right.$,解得$-\frac{1}{4}<λ<0$.
∴λ∈($-\frac{1}{4},0$).
②当λ=-1时,a2n=1,a2n-1=-3,
∴M=3,m=-1,不满足条件.
③当λ<-1时,当n→+∞时,a2n→+∞,无最大值;
当n→+∞时,a2n-1→-∞,无最小值.
综上所述,λ∈(-$\frac{1}{4}$,0)时满足条件.
点评 本题考查了数列递推式,考查了等差关系的确定,考查了数列的函数特性,训练了累加法求数列的通项公式,对(3)的求解运用了极限思想方法,是中档题.

| A. | $\frac{1+2ln2}{4}$ | B. | $\frac{3-2ln2}{4}$ | C. | $\frac{1+ln2}{2}$ | D. | $\frac{1-ln2}{2}$ |
| A. | -$\frac{1}{5}$i | B. | $\frac{1}{5}$ | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$i |
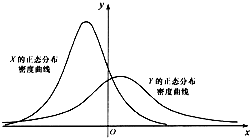 设X~N(μ1,σ12),Y~N(μ2,σ22),这两个正态分布密度曲线如图所示.下列结论中正确的是( )
设X~N(μ1,σ12),Y~N(μ2,σ22),这两个正态分布密度曲线如图所示.下列结论中正确的是( )| A. | P(Y≥μ2)≥P(Y≥μ1) | B. | P(X≤σ2)≤P(X≤σ1) | ||
| C. | 对任意正数t,P(X≤t)≥P(Y≤t) | D. | 对任意正数t,P(X≥t)≥P(Y≥t) |
 中,
中,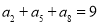 ,那么关于
,那么关于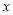 的方程:
的方程: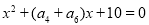 ( )
( )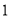 ,
,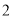 ,
,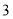 ,
,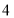 的四个大小相同的小球,现从这个盒子中,有放回地先后取得两个小球,其标号分别为
的四个大小相同的小球,现从这个盒子中,有放回地先后取得两个小球,其标号分别为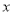 ,
,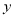 .
.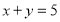 的概率;
的概率;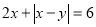 的概率.
的概率.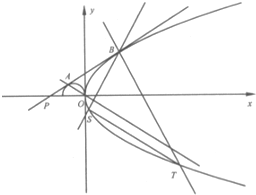 已知抛物线C:y2=2px(p>0),半圆M:x2+2x+y2=0(y≥0),过点P(-3,0)与半圆M相切于点A的直线l,与抛物线C有且只有一个公共点B.
已知抛物线C:y2=2px(p>0),半圆M:x2+2x+y2=0(y≥0),过点P(-3,0)与半圆M相切于点A的直线l,与抛物线C有且只有一个公共点B.