题目内容
3.若$\sqrt{\frac{1-sinx}{1+sinx}}$=$\frac{sinx-1}{cosx}$,则x的取值范围是$\frac{π}{2}$+2kπ<x<$\frac{3π}{2}$+2kπ(k∈Z).分析 利用同角三角函数间的基本关系得到sin2x+cos2x=1,整理得到关系式,已知等式利用二次根式性质及绝对值的代数意义化简,确定出cosx小于0,利用余弦函数性质即可确定出x的范围.
解答 解:∵sin2x+cos2x=1,即cos2x=1-sin2x=(1+sinx)(1-sinx),
∴$\frac{cosx}{1+sinx}$=$\frac{1-sinx}{cosx}$,
∵$\sqrt{\frac{1-sinx}{1+sinx}}$=$\sqrt{\frac{1-si{n}^{2}x}{(1+sinx)^{2}}}$=$\frac{|cosx|}{1+sinx}$=$\frac{sinx-1}{cosx}$,
∴cosx<0,
∴x的范围为$\frac{π}{2}$+2kπ<x<$\frac{3π}{2}$+2kπ(k∈Z).
故答案为:$\frac{π}{2}$+2kπ<x<$\frac{3π}{2}$+2kπ(k∈Z)
点评 此题考查了同角三角函数基本关系的运用,以及余弦函数的性质,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
13.已知函数f(x)在R上是增函数,若a+b>0,则( )
| A. | f(a)+f(b)>f(-a)+f(-b) | B. | f(a)+f(b)>f(-a)-f(-b) | C. | f(a)+f(-a)>f(b)-f(-b) | D. | f(a)+f(-a)>f(b)-f(-b) |
14.已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},B⊆A,则m的取值范围是( )
| A. | m<2 | B. | m<3 | C. | 2<m≤3 | D. | m≤3 |
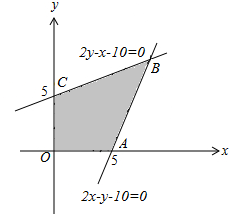 如图.已知线性规划的可行域是由直线x=0,y=0,2y-x-10=0和2x-y-10=0围成的四边形.若点B是使目标函数z=ax+y取最大值的点.求a的取值范围.
如图.已知线性规划的可行域是由直线x=0,y=0,2y-x-10=0和2x-y-10=0围成的四边形.若点B是使目标函数z=ax+y取最大值的点.求a的取值范围.