题目内容
(本大题满分12分)
已知数列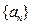 ,
,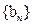 的通项公式分别为
的通项公式分别为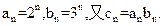
(I) 求证数列{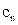 }是等比数列;
}是等比数列;
(II) 求数列{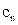 }的前n项和为
}的前n项和为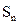 。
。
已知数列
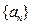 ,
,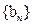 的通项公式分别为
的通项公式分别为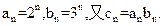
(I) 求证数列{
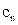 }是等比数列;
}是等比数列;(II) 求数列{
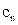 }的前n项和为
}的前n项和为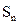 。
。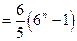
(I)证明:∵ 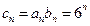 ,
, 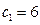 ,
,
∴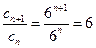 ,且
,且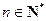 .……………4分
.……………4分
由此可得数列 是以首项为
是以首项为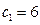 ,公比为
,公比为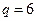 的等比数列.…………………6分
的等比数列.…………………6分
(II)由(I)可知
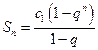
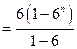 .……………9分
.……………9分
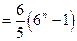 …………………12分
…………………12分
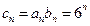 ,
, 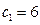 ,
,∴
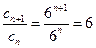 ,且
,且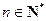 .……………4分
.……………4分由此可得数列
 是以首项为
是以首项为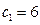 ,公比为
,公比为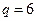 的等比数列.…………………6分
的等比数列.…………………6分(II)由(I)可知
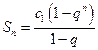
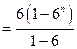 .……………9分
.……………9分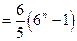 …………………12分
…………………12分
练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 12分)已知等差数列{an2
12分)已知等差数列{an2 }中,首项a12=1,公差d=1,an>0,n∈N
}中,首项a12=1,公差d=1,an>0,n∈N *.
*.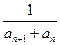 ,数列{bn}的前120项和T120;
,数列{bn}的前120项和T120; 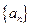 第10项为24,第25项为
第10项为24,第25项为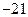 ,
,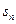 为其前n项和,求使
为其前n项和,求使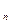 是公差不为0的等差数列
是公差不为0的等差数列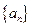 的前n项和,且
的前n项和,且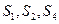 成等比数列。
成等比数列。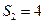 ,求
,求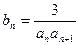 ,
,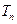 是数列
是数列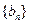 的前n项和,求使得
的前n项和,求使得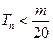 对所有
对所有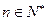 都成立的最小正整数m。
都成立的最小正整数m。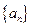 是等差数列,
是等差数列,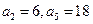 ;数列
;数列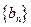 的前n项和是
的前n项和是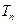 ,且
,且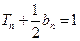 .
.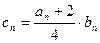 ,求
,求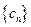 的前n项和
的前n项和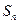
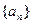 (n∈Z*)的前12项,
(n∈Z*)的前12项,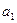
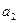
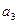
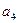
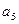
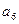
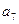
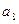
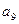
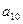

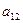
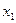
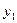
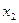
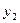
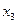
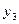
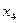
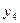
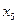
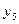
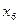
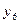
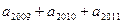 = ▲ .
= ▲ .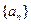 的通项
的通项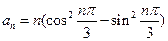 ,其前
,其前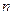 项和为
项和为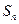 ,则
,则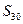 =____★____.
=____★____.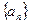 ,
,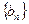 的前n项和分别为
的前n项和分别为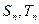 ,且
,且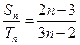 则
则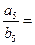 ( )
( )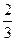
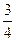
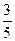
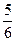
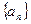 中,
中,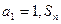 是数列
是数列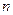 项和,对任意
项和,对任意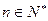 ,有
,有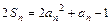 ,则数列
,则数列