题目内容
(本题满分12分)已知数列 是等差数列,
是等差数列,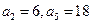 ;数列
;数列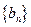 的前n项和是
的前n项和是 ,且
,且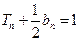 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求证:数列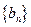 是等比数列;
是等比数列;
(3)记 ,求
,求 的前n项和
的前n项和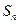
 是等差数列,
是等差数列,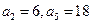 ;数列
;数列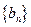 的前n项和是
的前n项和是 ,且
,且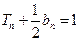 .
.(1)求数列
 的通项公式;
的通项公式;(2)求证:数列
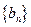 是等比数列;
是等比数列;(3)记
 ,求
,求 的前n项和
的前n项和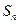
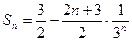
解:(1)设 的公差为
的公差为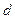 ,则:∵
,则:∵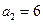 ,
, ,∴
,∴ , ……1分
, ……1分
∴ . ……2分
. ……2分
∴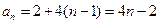 . ……3分
. ……3分
(2)当 时,
时, ,由
,由 ,得
,得 . ……4分
. ……4分
当 时,
时,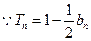 ,
,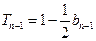 ,
,
∴ ,即
,即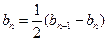 . ……6分
. ……6分
∴ .∴
.∴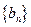 是以
是以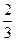 为首项,
为首项, 为公比的等比数列. ……7分
为公比的等比数列. ……7分
(3)由(2)可知: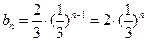 . ……8分
. ……8分
∴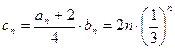 . ……9分
. ……9分
∴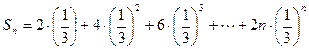 ①
①
∴ ② ……10分
② ……10分
.
∴①-②得
 ……11分
……11分
∴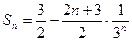 ……12分
……12分
 的公差为
的公差为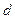 ,则:∵
,则:∵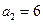 ,
, ,∴
,∴ , ……1分
, ……1分∴
 . ……2分
. ……2分∴
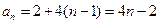 . ……3分
. ……3分(2)当
 时,
时, ,由
,由 ,得
,得 . ……4分
. ……4分当
 时,
时,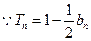 ,
,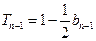 ,
,∴
 ,即
,即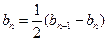 . ……6分
. ……6分∴
 .∴
.∴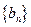 是以
是以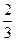 为首项,
为首项, 为公比的等比数列. ……7分
为公比的等比数列. ……7分(3)由(2)可知:
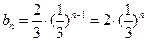 . ……8分
. ……8分∴
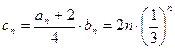 . ……9分
. ……9分∴
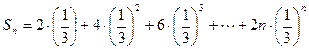 ①
①∴
 ② ……10分
② ……10分.
∴①-②得

 ……11分
……11分∴
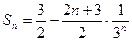 ……12分
……12分
练习册系列答案
相关题目
 ,
, 的通项公式分别为
的通项公式分别为
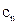 }是等比数列;
}是等比数列; 。
。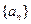 的前
的前 项和为
项和为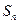 ,点
,点 在直线
在直线 上;数列
上;数列 满足
满足 ,且
,且 ,它的前9项和为153.
,它的前9项和为153.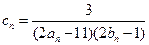 ,求数列
,求数列 的前
的前 .
. 的前
的前 项和为
项和为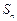 ,且满足
,且满足
 .
. ,
, ,
, ,
,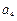 的值并猜想这个数列的通项公式
的值并猜想这个数列的通项公式 上有三点
上有三点 、
、 、
、 与右焦点
与右焦点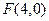 的距离成等差数列,则
的距离成等差数列,则 的值为( )
的值为( )
 满足
满足 ,则
,则 等于
等于
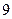
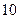

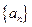 中,
中,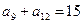 ,
,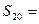
 中,
中, =1,
=1, ,则
,则 的值为 ★ .
的值为 ★ .