题目内容
(I)证明当
(II)若不等式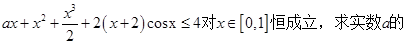 取值范围.
取值范围.

(II)若不等式
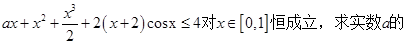 取值范围.
取值范围.(I)见解析(II)

(I)令 ,
,
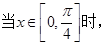
 即
即 为增函数,
为增函数,
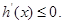 即
即 为减函数,
为减函数,

 故,
故, 为减函数,
为减函数,

(II)



下面证明,







综上
直接移项构造函数,比较容易想到,但是求出导函数后又变得无从下手,这时候需要二次求导分析来解决。两种解法各有特点。第二问主要是在第一问的基础上利用不等式进行适当的放缩,转化为另一个函数进行分析解答。
【考点定位】本题考查函数与导数,导数与不等式的综合应用。
 ,
,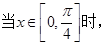
 即
即 为增函数,
为增函数,
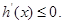 即
即 为减函数,
为减函数,
 故,
故, 为减函数,
为减函数,

(II)




下面证明,








综上

直接移项构造函数,比较容易想到,但是求出导函数后又变得无从下手,这时候需要二次求导分析来解决。两种解法各有特点。第二问主要是在第一问的基础上利用不等式进行适当的放缩,转化为另一个函数进行分析解答。
【考点定位】本题考查函数与导数,导数与不等式的综合应用。

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
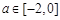 , 已知函数
, 已知函数
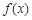 在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增;
在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增; 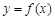 在点
在点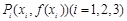 处的切线相互平行, 且
处的切线相互平行, 且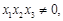 证明
证明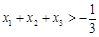 .
.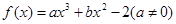 有且仅有两个不同的零点
有且仅有两个不同的零点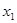 ,
,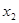 ,则( )
,则( ) 时,
时, ,
,
 ,
,
 时,
时,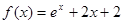 的零点所在区间是
的零点所在区间是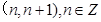 ,则
,则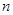 的值是______.
的值是______.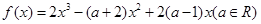 .
.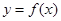 在
在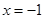 处的切线方程为
处的切线方程为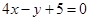 ,求实数
,求实数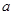 的值.
的值.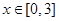 时,不等式
时,不等式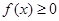 恒成立,求实数
恒成立,求实数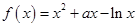 .
.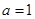 ,试求函数
,试求函数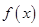 的单调区间;
的单调区间;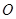 作曲线
作曲线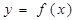 的切线,证明:切点的横坐标为1;
的切线,证明:切点的横坐标为1;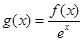 ,若函数
,若函数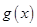 在区间(0,1]上是减函数,求
在区间(0,1]上是减函数,求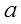 的取值范围.
的取值范围.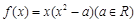 ,
,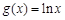 .
.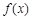 在
在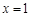 处取得极值,求
处取得极值,求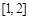 上
上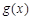 图像的上方(没有公共点),求实数
图像的上方(没有公共点),求实数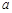 的取值范围.
的取值范围. 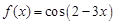 的导数等于
的导数等于 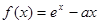 ,其中
,其中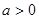 .
.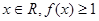 恒成立,求
恒成立,求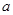 的取值范围;
的取值范围;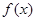 的图像上取定两点
的图像上取定两点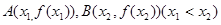 ,记直线
,记直线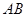 的斜率为
的斜率为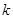 ,证明:存在
,证明:存在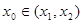 ,使
,使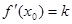 成立.
成立.