题目内容
14.已知{an}满足下列条件,写出前5项,数列的一个通项公式.(1)a1=2,an+1=3an+2;
(2)a1=2,an+1=3an+3
(3)a1=1,an+1=$\frac{2{a}_{n}}{{a}_{n}+2}$;
(4)a1=2,an+1=3an2.
分析 根据数列的递推关系进行递推即可.
解答 解:(1)∵a1=2,an+1=3an+2;
∴a2=3a1+2=6+2=8;
a3=3a2+2=24+2=26;
a4=3a3+2=78+2=80;
a5=3a4+2=240+2=242;
则an=3n-1.
(2)∵a1=2,an+1=3an+3,
∴a2=3a1+2=6+3=9;
a3=3a2+3=27+3=30;
a4=3a3+3=90+3=93;
a5=3a4+3=279+3=282;
an=$\frac{7}{2}$•3n-1-$\frac{3}{2}$.
(3)∵a1=1,an+1=$\frac{2{a}_{n}}{{a}_{n}+2}$;
∴a2=$\frac{2}{1+2}$=$\frac{2}{3}$;a3=$\frac{2×\frac{2}{3}}{\frac{2}{3}+2}$=$\frac{1}{2}$=$\frac{2}{4}$;
a4=$\frac{2×\frac{1}{2}}{\frac{1}{2}+2}=\frac{2}{5}$;
a5=$\frac{2×\frac{2}{5}}{\frac{2}{5}+2}$=$\frac{1}{3}$=$\frac{2}{6}$;
则an=$\frac{2}{n+1}$
(4)∵a1=2,an+1=3an2.
∴a2=3×22;
a3=3×(3×22)2=33×24
a4=3×(33×24)2=37×28;
a5=3×(37×28)2=315×216;
an=${3}^{{2}^{n-1}-1}•{2}^{{2}^{n}-1}$;
点评 本题主要考查数列的递推公式的应用,考查学生的运算能力.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
6.若函数f(x)=4x+5,则f-1(x+1)的定义域是( )
| A. | (4,+∞) | B. | (5,+∞) | C. | (-∞,4) | D. | (-∞,5) |
4.等差数列{an}中,前n项和为Sn,若Sk=25,S2k=100.则S3k=( )
| A. | 125 | B. | 200 | C. | 225 | D. | 250 |
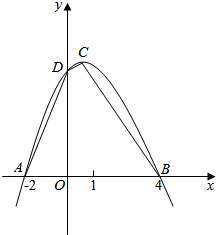 已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点.且函数的最大值为9,求二次函数的解析式.
已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点.且函数的最大值为9,求二次函数的解析式.