题目内容
13.已知sinθ-cosθ=$\frac{1}{5}$,θ∈(0,π),则tan(3π+θ)=$\frac{4}{3}$.分析 已知等式两边平方,利用完全平方公式及同角三角函数间基本关系化简,整理求出2sinθcosθ的值,再利用完全平方公式及同角三角函数间的基本关系变形求出sinθ+cosθ的值,与已知等式联立求出sinθ与cosθ的值,进而求出tanθ的值,原式利用诱导公式化简后代入计算即可求出值.
解答 解:把sinθ-cosθ=$\frac{1}{5}$①,两边平方得:(sinθ-cosθ)2=1-2sinθcosθ=$\frac{1}{25}$,即2sinθcosθ=$\frac{24}{25}$>0,
∵θ∈(0,π),
∴sinθ>0,cosθ>0,即sinθ+cosθ>0,
∴(sinθ+cosθ)2=1+2sinθcosθ=$\frac{49}{25}$,即sinθ+cosθ=$\frac{7}{5}$②,
联立①②,解得:sinθ=$\frac{4}{5}$,cosθ=$\frac{3}{5}$,
∴tanθ=$\frac{4}{3}$,
则原式=tanθ=$\frac{4}{3}$,
故答案为:$\frac{4}{3}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知点A(a,-5),B(0,10)间的距离是17,则a的值是( )
| A. | 8 | B. | -8 | C. | ±4 | D. | ±8 |
1.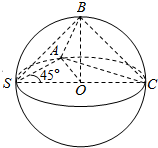 已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为( )
已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为( )
 已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为( )
已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{5\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
18.若正数x,y满足$\frac{1}{x}$+$\frac{9}{y}$=1,则xy的( )
| A. | 最大值为6 | B. | 最小值为6 | C. | 最大值为36 | D. | 最小值为36 |