题目内容
4.已知点P(x,y)的坐标x,y满足$\left\{\begin{array}{l}{\sqrt{3}x-y≤0}\\{x-\sqrt{3}y+2≥0}\\{y≥0}\end{array}\right.$,则x2+y2-4x的最大值是12.分析 先根据约束条件画出可行域,再利用几何意义求最值Z=x2+y2-4x的最大表示动点到定点(2,0)点的距离的平方有关,只需求出可行域内的动点到该点的距离最大值即可.
解答 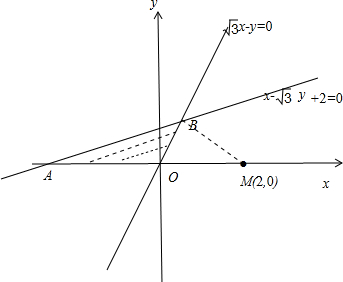 解:作出可行域,如图:
解:作出可行域,如图:
令z=x2+y2-4x=(x-2)2+y2-4,
∵(x-2)2+y2所表示的几何意义是动点到定点(2,0)的距离的平方,
作出可行域:
易知当为A点时取得目标函数的最大值,
可知A点的坐标为(-2,0),
代入目标函数中,可得zmax=12.
故答案为:12.
点评 本题属于线性规划中的延伸题,对于可行域不要求线性目标函数的最值,而是求可行域内的点与原点之间的距离问题.

练习册系列答案
相关题目
14.已知实数x、y满足$\left\{\begin{array}{l}{x≥1}\\{y≥0}\\{x-y≥0}\end{array}\right.$ 则z=$\frac{y-1}{x}$的取值范围是( )
| A. | [-1,0] | B. | [-1,1) | C. | (-∞,0] | D. | [-1,+∞) |
15.双曲线$\frac{x^2}{16}-\frac{y^2}{9}$=1与双曲线$\frac{x^2}{16-t}-\frac{y^2}{t+9}$=1(-9<t<16 )的( )
| A. | 实轴长相等 | B. | 虚轴长相等 | C. | 焦距相等 | D. | 离心率相等 |
12.函数f(x)=-2sin2x+2cos x的最小值和最大值分别是( )
| A. | -2,2 | B. | -2,$\frac{5}{2}$ | C. | -$\frac{1}{2}$,2 | D. | -$\frac{5}{2}$,2 |
16.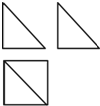 利用一球体毛坯切削后得到一个几何体,该几何体的三视图如图所示,若主视图和左视图都是直角边长为1的等腰直角三角形,则毛坯球体的体积最小应为( )
利用一球体毛坯切削后得到一个几何体,该几何体的三视图如图所示,若主视图和左视图都是直角边长为1的等腰直角三角形,则毛坯球体的体积最小应为( )
 利用一球体毛坯切削后得到一个几何体,该几何体的三视图如图所示,若主视图和左视图都是直角边长为1的等腰直角三角形,则毛坯球体的体积最小应为( )
利用一球体毛坯切削后得到一个几何体,该几何体的三视图如图所示,若主视图和左视图都是直角边长为1的等腰直角三角形,则毛坯球体的体积最小应为( )| A. | $\frac{{\sqrt{2}π}}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{\sqrt{3}π}{2}$ | D. | $\frac{8\sqrt{2}π}{3}$ |