题目内容
(满分20分)本题有2小题,第1小题12分,第2小题8分.
设 为定义域为
为定义域为 的函数,对任意
的函数,对任意 ,都满足:
,都满足: ,
, ,且当
,且当 时,
时,
(1)请指出 在区间
在区间 上的奇偶性、单调区间、最大(小)值和零点,并运用相关定义证明你关于单调区间的结论;
上的奇偶性、单调区间、最大(小)值和零点,并运用相关定义证明你关于单调区间的结论;
(2)试证明 是周期函数,并求其在区间
是周期函数,并求其在区间 上的解析式.
上的解析式.
设
 为定义域为
为定义域为 的函数,对任意
的函数,对任意 ,都满足:
,都满足: ,
, ,且当
,且当 时,
时,
(1)请指出
 在区间
在区间 上的奇偶性、单调区间、最大(小)值和零点,并运用相关定义证明你关于单调区间的结论;
上的奇偶性、单调区间、最大(小)值和零点,并运用相关定义证明你关于单调区间的结论;(2)试证明
 是周期函数,并求其在区间
是周期函数,并求其在区间 上的解析式.
上的解析式.略
解:(1)偶函数;.………………………………………………………………………1分
最大值为
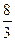 、最小值为0;.…………….……………………………………………………1分
、最小值为0;.…………….……………………………………………………1分单调递增区间:
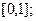 单调递减区间:
单调递减区间: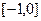 ;...…………………………………………1分
;...…………………………………………1分零点:
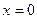 ..…………………………..……………………………………………………1分
..…………………………..……………………………………………………1分单调区间证明:
当
 时,
时,
设
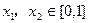 ,
,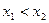 ,
,
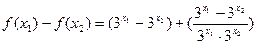
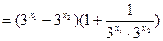
证明
 在区间
在区间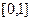 上是递增函数
上是递增函数由于函数
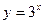 是单调递增函数,且
是单调递增函数,且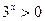 恒成立,
恒成立,所以
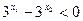 ,
,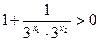 ,
,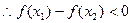
所以,
 在区间
在区间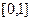 上是增函数.…………………………………………………….4分
上是增函数.…………………………………………………….4分证明
 在区间
在区间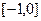 上是递减函数
上是递减函数【证法一】因为
 在区间
在区间 上是偶函数.
上是偶函数.对于任取的
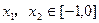 ,
,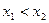 ,有
,有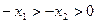
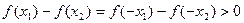
所以,
 在区间
在区间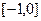 上是减函数.…………………………………………………..4分
上是减函数.…………………………………………………..4分【证法二】设
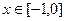 ,由
,由 在区间
在区间 上是偶函数,得
上是偶函数,得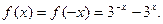
以下用定义证明
 在区间
在区间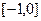 上是递减函数………………………………………..4分
上是递减函数………………………………………..4分(2)设
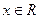 ,
,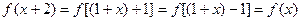 ,
,所以,2是
 周期. ……………………………………………………………4分
周期. ……………………………………………………………4分当
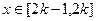 时,
时,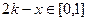 ,
,所以
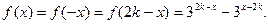 ………………………………………….4分
………………………………………….4分
练习册系列答案
相关题目
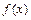 是以2为周期的周期函数,当
是以2为周期的周期函数,当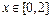 时,
时,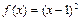 .
.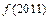 的值;
的值;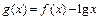 ,求函数
,求函数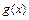 的零点的个数.
的零点的个数.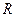 的奇函数
的奇函数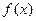 满足
满足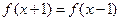 ,且当
,且当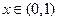 时,
时,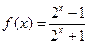 .
.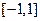 上的解析式;
上的解析式;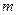 取何值时,方程
取何值时,方程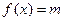 在
在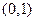 上有解?
上有解?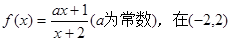 内为增函数,则实数a的取值范围
内为增函数,则实数a的取值范围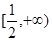
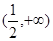
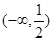
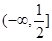
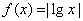 。若
。若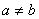 且
且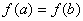 ,则
,则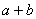 的取值范围是( )
的取值范围是( )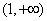
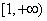
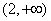
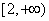
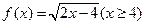 的反函数为( )
的反函数为( )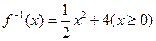

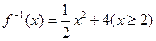
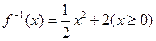
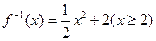
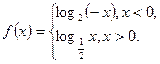 若
若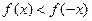 ,则实数
,则实数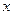 的取值范围是( )
的取值范围是( )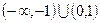


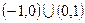
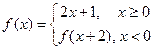 ,则
,则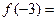 .
.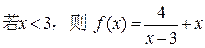 的最大值是 .
的最大值是 .