题目内容
9.函数y=-$\frac{1}{2}$sinx+1的值域是[$\frac{1}{2}$,$\frac{3}{2}$].分析 由条件利用正弦函数的值域,不等式的基本性质,求得函数y=-$\frac{1}{2}$sinx+1的值域.
解答 解:由sinx∈[-1,1],可得-$\frac{1}{2}$sinx∈[-$\frac{1}{2}$,$\frac{1}{2}$],∴y=-$\frac{1}{2}$sinx+1∈[$\frac{1}{2}$,$\frac{3}{2}$],
故答案为:[$\frac{1}{2}$,$\frac{3}{2}$].
点评 本题主要考查正弦函数的值域,不等式的基本性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在数列{an}中,若a1=1,an+1=3an+3n,(n≥1),则该数列的通项公式an=( )
| A. | n•3n | B. | n•3n-1 | C. | 3n | D. | 3n-1 |
19.求证:一个三角形中,至少有一个内角不小于60°,用反证法证明时的假设为“三角形的( )”.
| A. | 三个内角不都小于60° | B. | 三个内角都小于或等于60° | ||
| C. | 三个内角都大于60° | D. | 三个内角都小于60° |
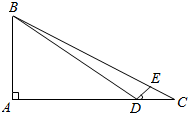 如图,在Rt△ABC中,∠A=90°,D、E分别是AC、BC上的点,且∠ADB=∠CDE=30°,BE=4CE,若CD=$\sqrt{3}$,那么BD的长为4.
如图,在Rt△ABC中,∠A=90°,D、E分别是AC、BC上的点,且∠ADB=∠CDE=30°,BE=4CE,若CD=$\sqrt{3}$,那么BD的长为4.