题目内容
19.已知3x2+2y2+4z2=24,求w=7x+y-5z的最值.分析 由柯西不等式,得[7x+y+(-5)z]2≤[($\frac{\sqrt{7}}{\sqrt{3}}$)2+($\frac{\sqrt{2}}{2}$)2+(-$\frac{5}{2}$)2](3x2+2y2+4z2),利用这个条件进行计算即可.
解答 解:由柯西不等式,得[7x+y+(-5)z]2≤[($\frac{\sqrt{7}}{\sqrt{3}}$)2+($\frac{\sqrt{2}}{2}$)2+(-$\frac{5}{2}$)2](3x2+2y2+4z2),
即(7x+y-5z)2≤$\frac{109}{12}$(3x2+2y2+4z2),…(5分)
即(7x+y-5z)2≤218
所以-$\sqrt{218}$≤7x+y-5z≤$\sqrt{218}$,
即w=7x+y-5z的最大值为$\sqrt{218}$,最小值为-$\sqrt{218}$.…(10分)
点评 本题考查柯西不等式在函数极值中的应用,关键是利用由柯西不等式,得[7x+y+(-5)z]2≤[($\frac{\sqrt{7}}{\sqrt{3}}$)2+($\frac{\sqrt{2}}{2}$)2+(-$\frac{5}{2}$)2](3x2+2y2+4z2).

练习册系列答案
相关题目
4.设a>|b|,且b<0,则( )
| A. | a+b>0 | B. | a+b<0 | C. | |a|<|b| | D. | b-a>0 |
11.设0<x<1,0<y<1,且x≠y,则x+y,2$\sqrt{xy}$,x2+y2,2xy中,最大的一个是( )
| A. | 2xy | B. | 2$\sqrt{xy}$ | C. | x2+y2 | D. | x+y |
8.下列函数中,最小正周期为π,且在区间[-$\frac{π}{4}$,0]上为增函数的是( )
| A. | y=cos2x | B. | y=-sin2x | C. | y=cos$\frac{x}{2}$ | D. | y=-sin$\frac{x}{2}$ |
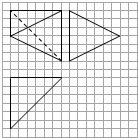 已知某几何体的三视图如图所示,求该几何体的体积.
已知某几何体的三视图如图所示,求该几何体的体积.