题目内容
若P(2,1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程是( )
| A.x-y-3=0 | B.2x+y-3=0 |
| C.x+y-3=0 | D.2x-y-5=0 |
C
由(x-1)2+y2=25知圆心为Q(1,0).据kQP · kAB=-1,
∴kAB=-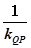 =-1(其中kQP=
=-1(其中kQP= =1).
=1).
∴AB的方程为y-1=-(x-2),
即x+y-3="0.∴" 应选C.
∴kAB=-
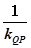 =-1(其中kQP=
=-1(其中kQP= =1).
=1).∴AB的方程为y-1=-(x-2),
即x+y-3="0.∴" 应选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,且与直线
,且与直线 平行的直线方程为 .
平行的直线方程为 .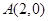 ,
,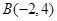 ,
,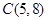 ,若线段
,若线段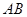 和
和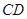 有相同的垂直平分线,则点
有相同的垂直平分线,则点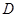 的坐标是( )
的坐标是( )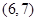
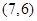


 与
与 互相平行,则
互相平行,则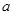 等于( )
等于( )
