题目内容
【题目】已知函数
,若存在
,使得关于
的方程
有三个不等实根,则实数
的取值范围为（ ）
A.
B.
C.
D.
【答案】B
【解析】
将
写成分段函数的形式，然后根据
与对称轴关系作分类讨论，再根据方程有解出参数
的取值范围.
因为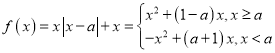
，且在
处两段函数值相同为，
又
即为
，
又
的对称轴为
，
的对称轴为
，
当
即
时（如图所示），在
上单调递增，在
上单调递增，
所以在
上单调递增，此时至多一解，不符合题意；
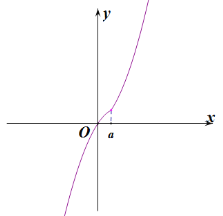
当
时（如图所示），在上单调递增，
在
上单调递减，在
上单调递增，
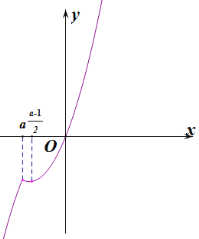
若有三解，则
，所以
，所以
，
因为存在满足条件，所以
，
又因为
在
上单调递增，所以
，所以
；
当
时（如图所示），在
上单调递增，在
上单调递减，
在上单调递增，
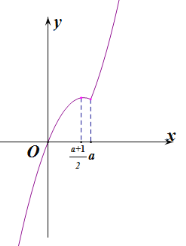
若有三解，则
，所以
，所以
，
因为存在满足条件，所以
，
又因为在
上单调递增，所以
，所以，
综上可知：.
故选：B.
练习册系列答案
小题狂做系列答案
相关题目
