题目内容
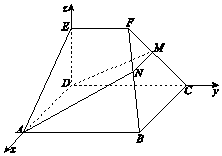
【题目】如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,AD⊥FC.点M在棱FC上,平面ADM与棱FB交于点N. 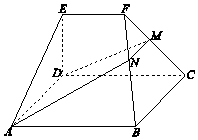
(Ⅰ)求证:AD∥MN;
(Ⅱ)求证:平面ADMN⊥平面CDEF;
(Ⅲ)若CD⊥EA,EF=ED,CD=2EF,平面ADE∩平面BCF=l,求二面角A﹣l﹣B的大小.
【答案】(Ⅰ)证明:因为ABCD为矩形,所以AD∥BC,
所以AD∥平面FBC.
又因为平面ADMN∩平面FBC=MN,
所以AD∥MN.
(Ⅱ)证明:因为ABCD为矩形,所以AD⊥CD.
因为AD⊥FC,
所以AD⊥平面CDEF.
所以平面ADMN⊥平面CDEF.
(Ⅲ)解:因为EA⊥CD,AD⊥CD,
所以CD⊥平面ADE,
所以CD⊥DE.
由(Ⅱ)得AD⊥平面CDEF,
所以AD⊥DE.
所以DA,DC,DE两两互相垂直.
建立空间直角坐标系D﹣xyz.
不妨设EF=ED=1,则CD=2,设AD=a(a>0).
由题意得,A(a,0,0),B(a,2,0),C(0,2,0),D(0,0,0),E(0,0,1),F(0,1,1).
所以 ![]() =(a,0,0),
=(a,0,0), ![]() =(0,﹣1,1).
=(0,﹣1,1).
设平面FBC的法向量为 ![]() =(x,y,z),则
=(x,y,z),则
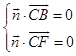 即
即 ![]() 令z=1,则y=1.
令z=1,则y=1.
所以 ![]() =(0,1,1).
=(0,1,1).
又平面ADE的法向量为 ![]() =(0,2,0),所以
=(0,2,0),所以
![]() =
= 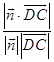 =
= ![]() .
.
因为二面角A﹣l﹣B的平面角是锐角,
所以二面角A﹣l﹣B的大小45°
【解析】(Ⅰ)通过证明AD∥BC,推出AD∥平面FBC,然后证明平AD∥MN.(Ⅱ)证明AD⊥CD,结合AD⊥FC,说明AD⊥平面CDEF,然后证明平面ADMN⊥平面CDEF.(Ⅲ)说明DA,DC,DE两两互相垂直,建立空间直角坐标系D﹣xyz,不妨设EF=ED=1,求出相关的坐标,求出平面FBC的法向量,平面ADE的法向量,通过向量的数量积求解二面角A﹣l﹣B的平面角的大小即可.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直.