题目内容
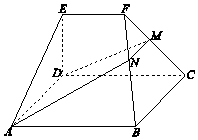
【题目】如图,四棱锥P﹣ABCD中,PD⊥平面PAB,AD∥BC,BC=CD= ![]() AD,E,F分别为线段AD,PD的中点.
AD,E,F分别为线段AD,PD的中点. 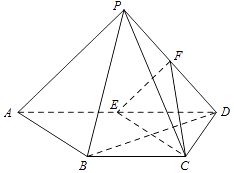
(Ⅰ)求证:CE∥平面PAB;
(Ⅱ)求证:PD⊥平面CEF;
(Ⅲ)写出三棱锥D﹣CEF与三棱锥P﹣ABD的体积之比.(结论不要求证明)
【答案】(Ⅰ)证明:∵BC∥AD,BC= ![]() ,E为AD中点,
,E为AD中点,
∴AE∥BC,且AE=BC,
∴四边形ABCE为平行四边形,
∴CE∥AB,
又AB平面PAB,CE平面PAB,
∴CE∥平面PAB.
(Ⅱ)证明:∵E、F分别为AD、PD的中点,∴EF∥PA,
又∵PD⊥平面PAB,PA,AB平面PAB,
∴PD⊥AB,PD⊥PA,∴PD⊥EF,
又CE∥AB,∴PD⊥CE,
∵EF∩CE=E,
∴PD⊥平面CEF.
(Ⅲ)解:三棱锥D﹣CEF与三棱锥P﹣ABD的体积之比为:
![]() =
= ![]() .
.
【解析】(Ⅰ)推导出四边形ABCE为平行四边形,从而CE∥AB,由此能证明CE∥平面PAB.(Ⅱ)推导出EF∥PA,则PD⊥AB,PD⊥PA,从而PD⊥EF,由CE∥AB,得PD⊥CE,由此能证明PD⊥平面CEF.(Ⅲ)由三棱锥的体积公式能求出三棱锥D﹣CEF与三棱锥P﹣ABD的体积之比.
【考点精析】掌握直线与平面平行的判定和直线与平面垂直的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目