题目内容
14.在风平浪静的海面上,有一战斗机要去执行一项紧急飞行任务,而航空母舰的弹射系统出了故障,无法在短时间内修复.已知飞机在跑道上加速时,可能产生的最大加速度为5m/s2,起飞速度为50m/s.跑道长为100m.经过计算发现在这些条件下飞机根本无法安全起飞(请你计算,作出判断).航空母舰不得不在海面上沿起飞方向运动,从而使飞机获得初速度,达到安全起飞的目的,那么航空母舰行驶的速度至少为多大?分析 根据匀变速直线运动的速度位移公式,结合初速度、加速度和末速度求出跑道的至少长度,根据匀变速直线运动的速度位移公式求出弹射系统使飞机具有的初速度.
解答 解:根据v2=2ax得,跑道的至少长度x=$\frac{{v}^{2}}{2a}$=$\frac{2500}{10}$=250m.100m<250m,
故在此条件下飞机根本无法安全起飞.
设航空母舰沿飞机起飞方向匀速航行速度为v1,在飞机起跑过程中的位移为x1,则有:x1=v1t,
飞机起跑过程中做初速度为V1的匀加速运动,设位移为x2,则有:x2=v1t+$\frac{1}{2}a{t}^{2}$,
运动的时间为:t=$\frac{v-{v}_{1}}{a}$,
由位移关系可知:L=x2-x1,
代入数据可得:v1=50-10$\sqrt{10}$m/s,
航空母舰行驶的速度至少为:50-10$\sqrt{10}$m/s.
点评 本题是匀变速直线运动的基本公式的直接应用,解决本题的关键掌握匀变速直线运动的速度位移公式,并能灵活运用,在第二问中,应该抓住二者的位移之差等于跑道的长度进行分析求解,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.当x∈[-1,t]时,函数f(x)=|x-2|+|5-x|的值域为[3,9],则实数t的取值范围是( )
| A. | [2,8] | B. | [2,4] | C. | [4,8] | D. | [-1,5] |

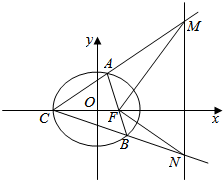 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F与抛物线y2=4x的焦点重合,D(1,$\frac{3}{2}$)是椭圆上一点,椭圆左顶点为C,过F的直线与椭圆交于A、B两点,直线CA、CB与直线1:x=4交于点M、N.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F与抛物线y2=4x的焦点重合,D(1,$\frac{3}{2}$)是椭圆上一点,椭圆左顶点为C,过F的直线与椭圆交于A、B两点,直线CA、CB与直线1:x=4交于点M、N.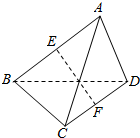 如图:在三棱锥A-BCD中,E,F分别是AB,CD的中点,且EF=5,AC=6,BD=8,则异面直线AC与BD的夹角为多少?
如图:在三棱锥A-BCD中,E,F分别是AB,CD的中点,且EF=5,AC=6,BD=8,则异面直线AC与BD的夹角为多少?