题目内容
7.已知函数f(x)=x2-alnx(a∈R).(1)若曲线f(x)在(1,f(1))处的切线与直线y=-x+5垂直,求实数a的值.
(2)?x0∈[1,e],使得$\frac{f({x}_{0})+1+a}{{x}_{0}}$≤0成立,求实数a的取值范围.
分析 (1)求出函数的导数,求得切线的斜率,由两直线垂直的条件:斜率之积为-1,即可得到所求a的值;
(2)由题意可得?x0∈[1,e],使得f(x0)+1+a≤0成立,运用参数分离和构造函数运用导数,判断单调性即可得到最小值,进而得到a的范围.
解答 解:(1)函数f(x)=x2-alnx的导数为f′(x)=2x-$\frac{a}{x}$,
即有曲线f(x)在(1,f(1))处的切线斜率为2-a,
由切线与直线y=-x+5垂直,可得2-a=1,
解得a=1;
(2)?x0∈[1,e],使得$\frac{f({x}_{0})+1+a}{{x}_{0}}$≤0成立,
即有?x0∈[1,e],使得f(x0)+1+a≤0成立,
由lnx0∈[0,1],则1-lnx0∈[0,1],
即有?x0∈[1,e],-a≥$\frac{{{x}_{0}}^{2}+1}{1-ln{x}_{0}}$的最小值,
由y=$\frac{{{x}_{0}}^{2}+1}{1-ln{x}_{0}}$的导数为y′=$\frac{{x}_{0}(3-2ln{x}_{0})+\frac{1}{{x}_{0}}}{(1-ln{x}_{0})^{2}}$,
由于3-2lnx0∈[1,3],则导数大于0,
即有函数y在[1,e]递增,
则函数的最小值为2,
即有-a≥2,解得a≤-2.
则实数a的取值范围是(-∞,-2].
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查函数的单调性的运用,注意存在性问题的解法,属于中档题.

练习册系列答案
相关题目
12.直线l交椭圆$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1与M,N两点,椭圆的上顶点为B点,若△BMN的重心坐标为($\frac{1}{3}$,$\frac{1}{3}$),则直线l的方程是( )
| A. | 2x-4y+3=0 | B. | 2x-4y-3=0 | C. | 4x-2y-3=0 | D. | x-y-5=0 |
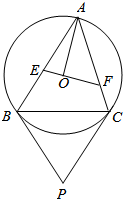 如图,锐角△ABC内接于圆0.过圆心0且垂直于半径0A的直线分别交边AB、AC于点E、F.设圆0在B、C两点处的切线相交于点P.求证:直线AP平分线段EF.
如图,锐角△ABC内接于圆0.过圆心0且垂直于半径0A的直线分别交边AB、AC于点E、F.设圆0在B、C两点处的切线相交于点P.求证:直线AP平分线段EF. 装潢师小王在墙面上设计了如图所示的一个图案,已知四边形四个顶点都在圆周上,且AD=DC=4m,BC=6m,∠A=120°,现在小王想买乳胶漆给四边形ABCD涂色,依据设计方案四边形的四边涂成红色,四边形内部要涂成蓝色,他想根据线段的长度与四边形的面积来买乳胶漆.请你帮他计算:
装潢师小王在墙面上设计了如图所示的一个图案,已知四边形四个顶点都在圆周上,且AD=DC=4m,BC=6m,∠A=120°,现在小王想买乳胶漆给四边形ABCD涂色,依据设计方案四边形的四边涂成红色,四边形内部要涂成蓝色,他想根据线段的长度与四边形的面积来买乳胶漆.请你帮他计算: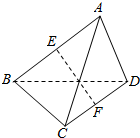 如图:在三棱锥A-BCD中,E,F分别是AB,CD的中点,且EF=5,AC=6,BD=8,则异面直线AC与BD的夹角为多少?
如图:在三棱锥A-BCD中,E,F分别是AB,CD的中点,且EF=5,AC=6,BD=8,则异面直线AC与BD的夹角为多少?