题目内容
20.已知集合M={(x,y)|x-3≤y≤x-1},N={P|PA≥$\sqrt{2}$PB,A(-1,0),B(1,0)},则表示M∩N的图形面积为$\frac{4π}{3}$+2$\sqrt{3}$.分析 建立坐标系:M为直线y=x-1和y=x-3之间的点的集合(含线上的点),N集合为以(3,0)为中心,半径为2$\sqrt{2}$的圆内的点的集合,联立方程组,求出点C,D的坐标,求出CD的长,再解直角三角形,求出扇形的圆心角,根据图形之间的面积,最后求出M∩N的图形面积.
解答 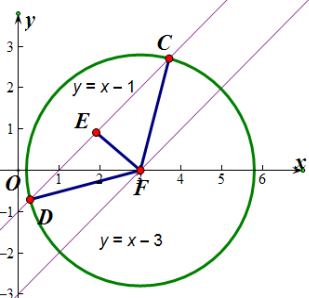 解:建立坐标系:M为直线y=x-1和y=x-3之间的点的集合(含线上的点),设P点的坐标为(x,y)
解:建立坐标系:M为直线y=x-1和y=x-3之间的点的集合(含线上的点),设P点的坐标为(x,y)
则可将PA≥$\sqrt{2}$PB表示成:$\sqrt{(x+1)^{2}+{y}^{2}}$≥$\sqrt{2}$$\sqrt{(x-1)^{2}+{y}^{2}}$,
∴(x+1)2+y2≥2[(x-1)2+y2],
∴(x-3)2+y2 ≤8,
即N集合为以(3,0)为中心,半径为2$\sqrt{2}$的圆内的点的集合,
则直线y=x-3经过圆心F,
过圆心F做FE⊥CD,垂足为E,
联立方程组得到$\left\{\begin{array}{l}{y=x-1}\\{(x-3)^{2}+{y}^{2}=8}\end{array}\right.$,
解得x=2±$\sqrt{3}$,y=1±$\sqrt{3}$,
则D(2-$\sqrt{3}$,1-$\sqrt{3}$),C(2+$\sqrt{3}$,1+$\sqrt{3}$),
∴|CD|2=(2+$\sqrt{3}$-2+$\sqrt{3}$)2+(1+$\sqrt{3}$-1+$\sqrt{3}$)2=24,即CD=2$\sqrt{6}$,
∴CE=$\frac{1}{2}$CD=$\sqrt{6}$,
在直角三角形CEF中,sinCFE=$\frac{CE}{CF}$=$\frac{\sqrt{6}}{2\sqrt{2}}$=$\frac{\sqrt{3}}{2}$,
∴∠CFE=60°,
∴∠CFD=120°,
∴S扇形CFD=$\frac{120}{360}$π×8=$\frac{8}{3}$π,S△CFD=$\frac{1}{2}$CF•DF•sin120°=$\frac{1}{2}$×8×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴S弓形=S扇形CFD-S△CFD=$\frac{8}{3}$π-2$\sqrt{3}$,
∵S半圆=$\frac{1}{2}$π×8=4π,
∴SM∩N的图形=S半圆-S弓形=4π-($\frac{8}{3}$π-2$\sqrt{3}$)=$\frac{4}{3}$π+2$\sqrt{3}$,
故答案为:$\frac{4}{3}$π+2$\sqrt{3}$.
点评 本题以集合的交集为载体,考查了直线和圆的位置关系,求出三角形,扇形,弓形的面积,属于中档题.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案| A. | a=$\frac{1}{3}$ | B. | a=1 | C. | a=2 | D. | a≤0 |
①?x∈N,x3<x2;
②所有可以被5整除的整数,末尾数字都是0;
③“若m>0,则x2+x-m=0有实根”的逆否命题;
④“若x2+y2≠0,则x,y不全为零”的否命题.
| A. | M>N | B. | M=N | C. | M<N | D. | 不确定. |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
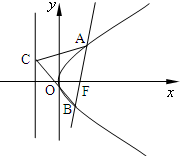 倾角为$\frac{π}{3}$的直线l过抛物线y2=4x的焦点F与抛物线交于A、B两点,点C是抛物线准线上的动点.
倾角为$\frac{π}{3}$的直线l过抛物线y2=4x的焦点F与抛物线交于A、B两点,点C是抛物线准线上的动点.